题目内容
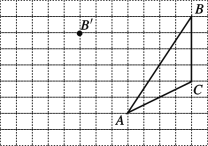
【题目】利用网格点和三角板画图或计算：
（1）在给定方格纸中画出平移后的
；
（2）画出
边上的中线
；
（3）画出
边上的高线
；
（4）的面积为_________；
（5）在图中能使
的格点
的个数有________个（点异于点
）．
【答案】87
【解析】
（1）直接利用平移的性质得出对应点位置进而得出答案；
（2）利用中线的定义找到
点位置，即可得出答案；
（3）利用高线的定义找到
点位置，即可得出答案；
（4）利用三角形面积求法得出答案；
（5）利用三角形面积求法得出符合题意的位置.
（1）如图所示：△A'B'C'即为所求；
（2）如图所示：中线CD即为所求；
（3）如图所示：高线AE即为所求；
（4）△A'B'C'的面积为：
；
故答案为：8；
（5）如图所示：在图中能使S△PAC=S△ABC的格点P的个数有7个．
故答案为：7．
阅读快车系列答案
【题目】小明统计了他家今年5月份打电话的次数及通话时间，并列出了频数分布表：
通话时间x/分钟 | 0＜x≤5 | 5＜x≤10 | 10＜x≤15 | 15＜x≤20 |
频数（通话次数） | 20 | 16 | 9 | 5 |
则5月份通话次数中，通话时间不超过15分钟的所占百分比是（ ）
A. 10% B. 40% C. 50% D. 90%
【题目】为了庆祝即将到来的“五四”青年节，某校举行了书法比赛，赛后随机抽查部分参赛同学的成绩，并制作成图表如下：
分数段 | 频数 | 频率 |
60≤x＜70 | 30 | 0.15 |
70≤x＜80 | m | 0.45 |
80≤x＜90 | 60 | n |
90≤x≤100 | 20 | 0.1 |
请根据以上图表提供的信息，解答下列问题：
（1）这次随机抽查了 名学生；表中的数m= ，n= ；
（2）请在图中补全频数分布直方图；
（3）若绘制扇形统计图，分数段60≤x＜70所对应扇形的圆心角的度数是 ；
（4）全校共有600名学生参加比赛，估计该校成绩80≤x＜100范围内的学生有多少人？
