题目内容
【题目】某单位需采购一批商品,购买甲商品10件和乙商品15件需资金350元,而购买甲商品15件和乙商品10件需要资金375元．
求甲、乙商品每件各多少元？
本次计划采购甲、乙商品共30件,计划资金不超过460元,
最多可采购甲商品多少件？
若要求购买乙商品的数量不超过甲商品数量的
,请给出所有购买方案,并求出该单位购买这批商品最少要用多少资金．
【答案】（1）甲商品每件17元，乙商品每件12元；（2）①最多可采购甲商品20件；②购买方案有四种，
方案一：甲商品20件，乙商品10件，此时花费为：20×17+10×12=460（元）；
方案二：甲商品19件，乙商品11件，此时花费为：19×17+11×12=455（元）；
方案三：甲商品18件，乙商品12件，此时花费为：18×17+12×12=450（元）；
方案四：甲商品17件，乙商品13件，此时花费为：17×17+13×12=445（元）.
即购买甲商品17件，乙商品13件时花费最少，最少要用445元．
【解析】
（1）根据题意可以列出相应的二元一次方程组，从而可以解答本题；
（2）根据题意可以列出相应的不等式，从而可以解答本题．
解：（1）设甲商品每件x元，乙商品每件y元，
，
解得，
，
即甲商品每件17元，乙商品每件12元；
（2）①设采购甲商品m件，
17m+12（30-m）≤460，
解得，m≤20，
即最多可采购甲商品20件；
②由题意可得，
，
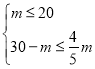解得，
，
∴购买方案有四种，
方案一：甲商品20件，乙商品10件，此时花费为：20×17+10×12=460（元），
方案二：甲商品19件，乙商品11件，此时花费为：19×17+11×12=455（元），
方案三：甲商品18件，乙商品12件，此时花费为：18×17+12×12=450（元），
方案四：甲商品17件，乙商品13件，此时花费为：17×17+13×12=445（元）.
即购买甲商品17件，乙商品13件时花费最少，最少要用445元．
