题目内容
【题目】如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( ) 
A.(4,2 ![]() )
)
B.(3,3 ![]() )
)
C.(4,3 ![]() )
)
D.(3,2 ![]() )
)
【答案】A
【解析】解:如图,作AM⊥x轴于点M. 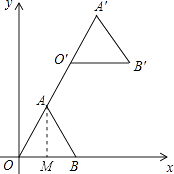
∵正三角形OAB的顶点B的坐标为(2,0),
∴OA=OB=2,∠AOB=60°,
∴OM= ![]() OA=1,AM=
OA=1,AM= ![]() OM=
OM= ![]() ,
,
∴A(1, ![]() ),
),
∴直线OA的解析式为y= ![]() x,
x,
∴当x=3时,y=3 ![]() ,
,
∴A′(3,3 ![]() ),
),
∴将点A向右平移2个单位,再向上平移2 ![]() 个单位后可得A′,
个单位后可得A′,
∴将点B(2,0)向右平移2个单位,再向上平移2 ![]() 个单位后可得B′,
个单位后可得B′,
∴点B′的坐标为(4,2 ![]() ),
),
故选A.
【考点精析】利用等边三角形的性质和坐标与图形变化-平移对题目进行判断即可得到答案,需要熟知等边三角形的三个角都相等并且每个角都是60°;新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点;连接各组对应点的线段平行且相等.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目