��Ŀ����
����Ŀ����ͼ����֪������ABCD�ı�BC��CD�Ϸֱ���E��F���㣬�ҡ�EAF=45�����ֽ���ADF�Ƶ�A˳ʱ����ת90������ABH��.
��1���߶�EF��BE��DF�к�������ϵ����˵�����ɣ�
ģ�£�1���еķ��������2������3���������⣺
��2����ͼ�ڣ�����E��F����BD�ϣ������������䣬��BE=![]() ��DF=3����EF�ij���
��DF=3����EF�ij���
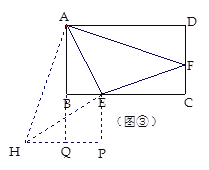
��3����ͼ�ۣ�ͼ�α�ɾ���ABCD����EAF=45�㣬BE=3��AB=6��AD=10����DF��EF�ij�.

���𰸡�(1) EF=BE+DF��(2) ![]() ��(3)
��(3) ![]() ��
��![]() .
.
�������������������1������ת�����ʵã���ADF�ա�ABH���Ӷ�����SAS֤��HAE�ա�FAE���õ�EF=HE���Ӷ��õ����ۣ�
��2���ѡ�ABE�Ƶ�A��ת90�㵽��ADG������GF��ͬ��1���ɵã���AGD�ա�AEB����AEF�ա�AGF���õ�BE=GD����GDA=��EBA=45�㣬EF=GF���ɡ�FDA=45�㣬�õ���FDG=90�㣮��Rt��GDF�У��ɹ��ɶ������ɵõ����ۣ�
��3���ѡ�ADF��A��ת90�㵽��AQH������EH����E��EP��HQ ��P��ͬ������ADF�ա�AQH����HAE�ա�FAE��EF=HE����DF=x����Rt��HPE��Rt��ECF�У��ɹ��ɶ������ɵó����ۣ�
����������⣺��1��EF=BE+DF���������£�
����ת�����ʵã���ADF�ա�ABH����AH=AF��DF=HB����HAB=��DAF���ߡ�DAF+��FAB=90�㣬���FAH=90�㣮�ߡ�EAF=45�㣬���EAH=45�㣬���EAF=��EAH���ڡ�EAF�͡�EAH�У���AF=AH����EAF=��HAE��AE=AE������HAE�ա�FAE��SAS������EF=HE����HE=HB+BE=DF+BE����EF=BE+DF��
��2���ѡ�ABE�Ƶ�A��ת90�㵽��ADG������GF��ͬ��1���ɵã���AGD�ա�AEB����AEF�ա�AGF����BE=GD����GDA=��EBA=45�㣬EF=GF���ߡ�FDA=45�㣬���FDG=90�㣬��EF=FG=![]() =
=![]() =
=![]() =
=![]() ��
��

��3���ѡ�ADF��A��ת90�㵽��AQH������EH����E��EP��HQ ��P��
ͬ������ADF�ա�AQH����HAE�ա�FAE��SAS������EF=HE��
��DF=x����Rt��HPE��Rt��ECF�У��ɹ��ɶ����ã�
![]() ��
��![]()
��![]()
![]() ��
��
��ã�![]()
![]() ����DF=
����DF=![]() ��EF=
��EF=![]() ��
��

����Ŀ���������Ϊ�Ӽס��������˶�Ա��ѡ��һ�˲μ�ʡ�����������ǽ��������β��ԣ����Գɼ��������λ��������
��һ�� | �ڶ��� | ������ | ���Ĵ� | ����� | ������ | |
�� | 10 | 8 | 9 | 8 | 10 | 9 |
�� | 10 | 7 | 10 | 10 | 9 | 8 |
��1�����ݱ����е����ݣ��ֱ����ס��ҵ�ƽ���ɼ���
��2����֪�����γɼ��ķ���S��2= ![]() ���Լ��������β��Գɼ��ķ�����ݣ�1������2������Ľ��������Ϊ�Ƽ�˭�μ�ʡ���������ʣ���˵�����ɣ�
���Լ��������β��Գɼ��ķ�����ݣ�1������2������Ľ��������Ϊ�Ƽ�˭�μ�ʡ���������ʣ���˵�����ɣ�


