题目内容
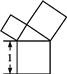
【题目】如图,已知E是正方形ABCD的边CD外的一点,△DCE为等边三角形,BE交对角线AC于F .
(1)求∠AFD的度数;
(2)求证:AF = EF.

【答案】∠AFD=60°;(2)证明见解析.
【解析】整体分析:
(1)用正方形和等边三角形的性质得△CDF≌△CBF,由△CBE是等腰三角形,求∠CBE的度数即可;(2)用SAS证明△ADF≌△EDF.
(1)解:∵四边形ABCD是正方形,
∴CB=CD=DA=DE,∠BCF=∠DCF=45°,∠BCD=90°,
∵CF=CF,
∴△CDF≌△CBF,
∴∠CDF=∠CBE,
∵△CDE是等边三角形,∴CB=CE,∠DCE=60°,
∴∠CBE=(180°-90°-60°)÷2=15°,
∴∠CDF=15°.
∴∠AFD=∠ACD+∠CDF=45°+15°=60°.
(2)证明:∵DA=DE,∠ADF=∠EDF=75°,DF=DF,
∴△ADF≌△EDF,
∴AF=EF.

练习册系列答案
相关题目