题目内容
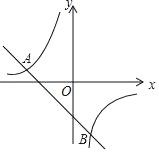
【题目】如图，一次函数y1＝kx+b（k≠0）和反比例函数
的图象相交于点A（﹣4，2），B（n，﹣4）
（1）求一次函数和反比例函数的表达式；
（2）观察图象，直接写出不等式y1＜y2的解集．
【答案】(1) y＝﹣x﹣2，;(2) x＞2或﹣4＜x＜0
【解析】
将点A（﹣4，2）代入
，求反比例函数解析式，再求得B的坐标，将A与B两点坐标代入y1＝kx+b，即可求解；
（2）y1＜y2，在图象中找反比例函数图象在一次函数图象上方的部分即可.
（1）将点A（﹣4，2）代入，
∴m＝﹣8，
∴y＝
，
将B（n，﹣4）代入y＝，
∴n＝2，
∴B（2，﹣4），
将A（﹣4，2），B（2，﹣4）代入y1＝kx+b，
得到
，
∴
，
∴y＝﹣x﹣2，
（2）由图象直接可得：x＞2或﹣4＜x＜0；
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
【题目】某学校在A、B两个校区各有九年级学生200人，为了解这两个校区九年级学生的教学学业水平的情况，进行了抽样调查，过程如下，请补充完整．
收集数据：从A、B两个校区各随机抽取20名学生，进行了数学学业水平测试，测试成绩（百分制）如下：
A校区 86 74 78 81 76 75 86 70 75 90
75 79 81 70 74 80 87 69 83 77
B校区 80 73 70 82 71 82 83 93 77 80
81 93 81 73 88 79 81 70 40 83
整理、描述数据 按如下分数段整理、描述这两组样本数据：
成绩x 人数 校区 | 40≤x＜50 | 50≤x＜60 | 60≤x＜70 | 70≤x＜80 | 80≤x＜90 | 90≤x≤100 |
A | 0 | 0 | 1 | 11 | 7 | 1 |
B |
（说明：成绩80分及以上的学业水平优秀，70﹣79分为淡定业水平良好，60﹣69分为学业水平合格，60分以下为学业水平不合格）
分析数据 两组样本数据的平均数、中位数、众数如下表所示：
校区 | 平均数 | 中位数 | 众数 |
A | 78.3 | m | 75 |
B | 78 | 80.5 | 81 |
其中m＝ ；
得出结论：a．估计B校区九年级数学学业水平在优秀以上的学生人数为 ；
b．可以推断出 校区的九年级学生的数学学业水平较高，理由为 （至少从两个不同的角度说明推断的合理性）．
