题目内容
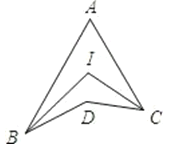
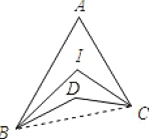
【题目】如图 ,BI、CI分别平分∠ABD和∠ACD,∠A=40°,∠D=160°,则∠I=___________
【答案】100°.
【解析】
连接BC,根据三角形内角和定理可得出∠DBC+∠DCB的度数,再根据∠A=40°求出∠ABC+∠ACB的度数,进而可得出∠ABD+∠ACD的度数,根据BI、CI分别平分∠ABD和∠ACD得出∠IBD+∠ICD的度数,进而可得出∠IBC+∠ICB的度数,由三角形内角和定理即可得出结论.
解:接BC,
∵∠D=160°,
∴∠DBC+∠DCB=180°160°=20°.
∵∠A=40°,
∴∠ABC+∠ACB=180°40°=140°,
∴∠ABD+∠ACD=140°20°=120°.
∵BI、CI分别平分∠ABD和∠ACD,
∴∠IBD+∠ICD=![]() (∠ABD+∠ACD)=
(∠ABD+∠ACD)=![]() ×120°=60°.
×120°=60°.
∴∠IBC+∠ICB=(∠IBD+∠ICD)+(∠DBC+∠DCB)=60°+20°=80°,
∴∠I=180°80°=100°.
故填:100°.

练习册系列答案
相关题目