题目内容
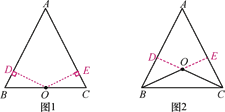
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.

(1)求证:△ABD是等腰三角形;
(2)若∠A=40°,求∠DBC的度数;
(3)若AE=6,△CBD的周长为20,求△ABC的周长.
【答案】(1)证明见解析;(2)30°;(3)32.
【解析】试题(1)根据线段的垂直平分线到线段两端点的距离相等即可得证;
(2)首先利用三角形内角和求得∠ABC的度数,然后减去∠ABD的度数即可得到答案;
(3)将△ABC的周长转化为AB+AC+BC的长即可求得.
试题解析:(1)∵AB的垂直平分线MN交AC于点D,
∴DB=DA,
∴△ABD是等腰三角形;
(2)∵△ABD是等腰三角形,∠A=40°,
∴∠ABD=∠A=40°,∠ABC=∠C=(180°-40°)÷2="70°"
∴∠DBC=∠ABC-∠ABD=70°-40°=30°;
(3)∵AB的垂直平分线MN交AC于点D,AE=6,
∴AB=2AE=12,
∵△CBD的周长为20,
∴AC+BC=20,
∴△ABC的周长=AB+AC+BC=12+20=32.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目