题目内容
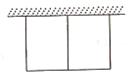
【题目】农贸市场拟建两间长方形储藏室,储藏室的一面靠墙(墙长30m),中间用一面墙隔开,如图所示,已知建筑材料可建墙的长度为42m,则这两间长方形储藏室的总占地面积的最大值为_______m2.
【答案】![]()
【解析】设中间隔开的墙EF的长为xm,建成的储藏室总占地面积为sm,根据题意可知AD的长度等于BC的长度,列出式子AD-2+3X=28,得出用x的代数式表示AD的长,再根据矩形的面积=AD·AB得出S关于x的解析式,再利用二次函数的性质即可求解.
设中间隔开的墙EF的长为xm,建成的储藏室总占地面积为sm,根据题意得AD+3x=42,解得AD=42-3x,则S=x(42-3x)= -3x+42x=-3(x-7)+147,故这两间长方形储藏室的总占地面积的最大值为:147m,故答案为:147.

练习册系列答案
相关题目
【题目】(本题满分10分)虽然近几年无锡市政府加大了太湖水治污力度,但由于大规模、高强度的经济活动和日益增加的污染负荷,使部分太湖水域水质恶化,富营养化不断加剧。为了保护水资源,我市制定一套节水的管理措施,其中对居民生活用水收费作如下规定:
月用水量(吨) | 单价(元/吨) |
不大于10吨部分 | 1.5 |
大于10吨不大于m吨部分(20≤m≤50) | 2 |
大于m吨部分 | 3 |
(1)若某用户六月份用水量为18吨,求其应缴纳的水费;
(2)记该用户六月份用水量为x吨,缴纳水费为y元,试列出y关于x的函数关系式;
(3)若该用户六月份用水量为40吨,缴纳水费y元的取值范围为70≤y≤90,试求m的取值范围.