题目内容
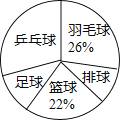
【题目】某中学为了了解学生最喜欢的一种球类运动,以便合理安排活动场地,在全校至少喜欢一种球类(乒乓球、羽毛球、排球、篮球、足球)运动的1800名学生中,随机抽取了若干名学生进行调查(每人只能在这五种球类运动中选择一种),调查结果统计如下:
球类名称 | 乒乓球 | 羽毛球 | 排球 | 篮球 | 足球 |
人数 | 42 | a | b | 33 | 21 |
解答下列问题:
(1)这次抽样调查的总人数是 ,统计表中a的值为 .
(2)求扇形统计图中排球一项的扇形圆心角度数.
(3)试估计全校1800名学生中最喜欢乒乓球运动的人数.
【答案】(1)150人,39;(2)36°;(3)504人.
【解析】
(1)用喜欢篮球的人数除以其所占的百分比即可求得调查的总人数,用调查的总人数乘以羽毛球所占的百分比即可求得a;
(2)用调查的总人数减去其他求得b值,求出排球所占百分比即可求得排球一项的扇形圆心角度数;
(3)用全校人数乘以喜欢乒乓球的人所占的百分比即可.
解:(1)∵喜欢篮球的有33人,占22%,
∴抽样调查的总人数为33÷22%=150(人);
∴a=150×26%=39(人);
故答案为:150人,39;
(2)b=150﹣42﹣39﹣33﹣21=15(人);
扇形统计图中排球一项的扇形圆心角度数为:360°×![]() =36°;
=36°;
(3)最喜欢乒乓球运动的人数为:1800×![]() =504(人).
=504(人).

【题目】为了庆祝“五四”青年节,我市某中学举行了书法比赛,赛后随机抽查部分参赛同学成绩(满分为100分),并制作成图表如下
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x≤100 | 20 | 0.1 |
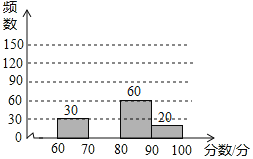
请根据以上图表提供的信息,解答下列问题:
(1)这次随机抽查了 名学生;表中的数m= ,n= ;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是 ;
(4)全校共有600名学生参加比赛,估计该校成绩不低于80分的学生有多少人?