题目内容
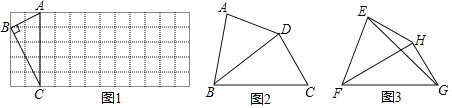
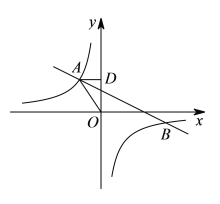
【题目】如图，在平面直角坐标系xOy中，Rt△OCD的一边OC在x轴上，∠OCD＝90°，点D在第一象限，OC＝6，DC＝4，反比例函数的图象经过OD的中点A．
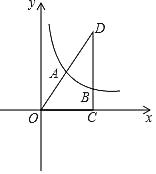
（1）求该反比例函数的解析式；
（2）若该反比例函数的图象与Rt△OCD的另一边DC交于点B，求过A、B两点的直线的解析式．
【答案】（1）
；（2）
.
【解析】
（1）先求出点A的坐标，再利用待定系数法求解可得；
（2）先求出点B的坐标，再利用待定系数法求解可得．
解：（1）∵∠OCD＝90°，点D在第一象限，OC＝6，DC＝4，
∴D（6，4），
∵OD的中点为点A，
∴A（3，2）；
设反比例函数解析式为
，
那么k＝3×2＝6，
∴该反比例函数的解析式为；
（2）在中，当x＝6时，y＝1，
则点B（6，1），
设直线AB解析式为y＝mx+n，（m
0）,代入A,B坐标得,
则
，
解得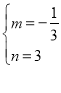
，
∴直线AB解析式为y＝﹣
x+3．
练习册系列答案
相关题目
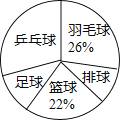
【题目】某中学为了了解学生最喜欢的一种球类运动，以便合理安排活动场地，在全校至少喜欢一种球类（乒乓球、羽毛球、排球、篮球、足球）运动的1800名学生中，随机抽取了若干名学生进行调查（每人只能在这五种球类运动中选择一种），调查结果统计如下：
球类名称 | 乒乓球 | 羽毛球 | 排球 | 篮球 | 足球 |
人数 | 42 | a | b | 33 | 21 |
解答下列问题：
（1）这次抽样调查的总人数是 ，统计表中a的值为 ．
（2）求扇形统计图中排球一项的扇形圆心角度数．
（3）试估计全校1800名学生中最喜欢乒乓球运动的人数．
