题目内容
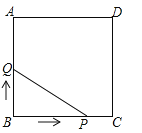
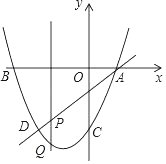
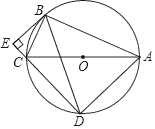
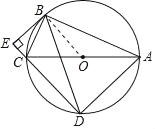
【题目】如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,BD=BA,BE⊥DC交DC的延长线于点E.
(1)若∠BAD=70°,则∠BCA= °;
(2)若AB=12,BC=5,求DE的长:
(3)求证:BE是⊙O的切线.
【答案】(1)70;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)根据等腰三角形的性质、圆周角定理解答;
(2)根据勾股定理求出AC,证明△DEB∽△ABC,根据相似三角形的性质列出比例式,代入计算,得到答案;
(3)连接OB,根据圆内接四边形的性质、圆周角定理、平行线的性质得到OB∥DE,根据平行线的性质得到BE⊥OB,根据切线的判定定理证明结论.
(1)解:∵BD=BA,
∴∠BDA=∠BAD=70°,
由圆周角定理得,∠BCA=∠BDA=70°,
故答案为:70;
(2)解:在Rt△ABC中,AC=![]() =13,
=13,
∠BDE=∠BAC,∠BED=∠CBA=90°,
∴△DEB∽△ABC,
∴![]() ,即
,即![]() ,
,
解得,DE=![]() ;
;
(3)证明:连接OB,
∵OB=OC,
∴∠OBC=∠OCB,
∵四边形ABCD内接于⊙O,
∴∠BAD+∠BCD=180°,
∵∠BCE+∠BCD=180°,
∴∠BCE=∠BAD,
∵BD=BA,
∴∠BDA=∠BAD,
∵∠BDA=∠ACB,
∴∠ACB=∠BAD,
∴∠OBC=∠BCE,
∴OB∥DE,
∵BE⊥DC,
∴BE⊥OB,
∴BE是⊙O的切线.

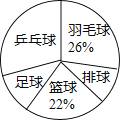
【题目】某中学为了了解学生最喜欢的一种球类运动,以便合理安排活动场地,在全校至少喜欢一种球类(乒乓球、羽毛球、排球、篮球、足球)运动的1800名学生中,随机抽取了若干名学生进行调查(每人只能在这五种球类运动中选择一种),调查结果统计如下:
球类名称 | 乒乓球 | 羽毛球 | 排球 | 篮球 | 足球 |
人数 | 42 | a | b | 33 | 21 |
解答下列问题:
(1)这次抽样调查的总人数是 ,统计表中a的值为 .
(2)求扇形统计图中排球一项的扇形圆心角度数.
(3)试估计全校1800名学生中最喜欢乒乓球运动的人数.