题目内容
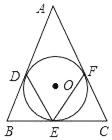
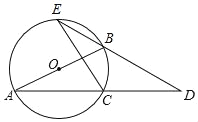
【题目】如图,AB是⊙O的直径,D是弦AC的延长线上一点,且CD=AC,DB的延长线交⊙O于点E.
(1)求证:CD=CE;
(2)连结AE,若∠D=25°,求∠BAE的度数.
【答案】(1)证明见解析;(2)40°.
【解析】
(1) 连接BC,利用直径所对的圆周角是直角、线段垂直平分线性质、同弧所对的圆周角相等、等角对等边即可证明.
(2)利用三角形外角等于不相邻的两个内角和、利用直径所对的圆周角是直角、直角三角形两锐角互余即可解答.
(1)证明:连接BC,
∵AB是⊙O的直径,
∴∠ABC=90°,即BC⊥AD,
∵CD=AC,
∴AB=BD,
∴∠A=∠D,
∴∠CEB=∠A,
∴∠CEB=∠D,
∴CE=CD.
(2)解:连接AE.
∵∠A BE=∠A+∠D=50°,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠BAE=90°﹣50°=40°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目