ЬтФПФкШн
ЁОЬтФПЁПЁїABCжаЃЌЁЯBAC=ІСЁуЃЌAB=ACЃЌDЪЧBCЩЯвЛЕуЃЌНЋADШЦЕуAЫГЪБеыа§зЊІСЁуЃЌЕУЕНЯпЖЮAEЃЌСЌНгBEЃЎ
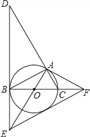
ЃЈ1ЃЉЃЈЬиР§ИажЊЃЉШчЭМ1ЃЌШєІС=90ЃЌдђBD+BEгыABЕФЪ§СПЙиЯЕЪЧ ЃЎ
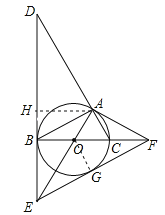
ЃЈ2ЃЉЃЈРрБШЬНОПЃЉШчЭМ2ЃЌШєІС=120ЃЌЪдЬНОПBD+BEгыABЕФЪ§СПЙиЯЕЃЌВЂжЄУїЃЎ
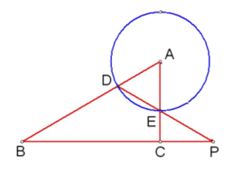
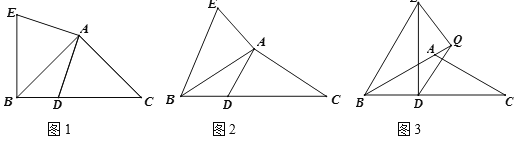
ЃЈ3ЃЉЃЈЭиеЙбгЩьЃЉШчЭМ3ЃЌШєІС=120ЃЌAB=AC=4ЃЌBD=![]() ЃЌQЮЊBAбгГЄЯпЩЯЕФвЛЕуЃЌНЋQDШЦЕуQЫГЪБеыа§зЊ120ЁуЃЌЕУЕНЯпЖЮQEЃЌDEЁЭBCЃЌЧѓAQЕФГЄЃЎ
ЃЌQЮЊBAбгГЄЯпЩЯЕФвЛЕуЃЌНЋQDШЦЕуQЫГЪБеыа§зЊ120ЁуЃЌЕУЕНЯпЖЮQEЃЌDEЁЭBCЃЌЧѓAQЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЌМћНтЮіЃЛЃЈ3ЃЉ
ЃЌМћНтЮіЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнSASПЩжЄЁїABEЁеЁїACDЃЌНјЖјПЩЕУBE=CDЃЌНсКЯBD+CD=BCПЩЕУBD+ BE=BCЃЌдйИљОнЕШбќжБНЧШ§НЧаЮжаBC=![]() МДПЩжЄЕУ
МДПЩжЄЕУ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЙ§ЕуAзїAHЁЭBCЃЌИљОнЁЯBAC=120ЁуЃЌAB=ACПЩЕУЁЯABC=30ЁуЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЃЌгЩЃЈ1ЃЉПЩжЊBD+ BE=BCЃЌгЩДЫМДПЩЕУ
ЃЌгЩЃЈ1ЃЉПЩжЊBD+ BE=BCЃЌгЩДЫМДПЩЕУ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЙ§QЕузїQFЁЮACНЛBCбгГЄЯпгкЕуFЃЌЯШжЄЁЯBQF =120ЁуЃЌBQ=QFЃЌНјЖјПЩгЩЃЈ2ЃЉЭЌРэПЩжЊЃЌЁїQBEЁеЁїQFDЃЌ![]() ЃЌНјЖјПЩжЄЕУ
ЃЌНјЖјПЩжЄЕУ![]() ЃЌдйИљОнcosЁЯEBD=
ЃЌдйИљОнcosЁЯEBD=![]() =cos60Ёу=
=cos60Ёу=![]() ПЩЧѓЕУ
ПЩЧѓЕУ![]() ЃЌНјЖјЧѓЕУ
ЃЌНјЖјЧѓЕУ![]() ЃЌзюКѓИљОнAQ=BQЃABМДПЩЕУЕНД№АИЃЎ
ЃЌзюКѓИљОнAQ=BQЃABМДПЩЕУЕНД№АИЃЎ
НтЃКЃЈ1ЃЉ![]()
РэгЩШчЯТЃК
ЁпЁЯEAD=ЁЯBAC=90Ёу
ЁрЁЯEAB=ЁЯDAC
дкЁїABEгыЁїACDжаЃЌ
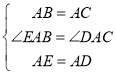
ЁрЁїABEЁеЁїACDЃЈSASЃЉ
ЁрBE=CDЃЌ
ЁпBD+CD=BC
ЁрBD+ BE=BC
ЁпдкRtЁїABCжаЃЌЁЯBAC=90ЁуЃЌAB=ACЃЌ
ЁрBC=![]()
ЁрBD+ BE=![]() ЃЛ
ЃЛ
ЃЈ2ЃЉНсТлЃК![]() ЃЌ
ЃЌ
РэгЩШчЯТЃК
Й§ЕуAзїAHЁЭBCЃЌ
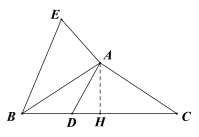
ЁпЁЯBAC=120ЁуЃЌAB=AC
ЁрЁЯABC=30ЁуЃЌ![]()
дкRtЁїABHжаЃЌcosЁЯABH=![]() =cos30Ёу=
=cos30Ёу=![]()
ЁрBH=![]() ABЃЌ
ABЃЌ
Ёр![]()
гЩЃЈ1ЃЉЭЌРэПЩжЊBD+ BE=BCЃЌ
Ёр![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЙ§QЕузїQFЁЮACНЛBCбгГЄЯпгкЕуFЃЌ

![]()
Ёр![]()
ЁрЁЯQFC=ЁЯQBF =30ЁуЃЌЁЯBQF =120Ёу
ЁрBQ=QF
гЩЃЈ2ЃЉЭЌРэПЩжЊЃЌЁїQBEЁеЁїQFDЃЌ![]()
![]()
![]()
![]()
ЁрcosЁЯEBD=![]() =cos60Ёу=
=cos60Ёу=![]()
![]()
Ёп![]()
![]()
![]() ЃЌ
ЃЌ
ЁрAQ=BQЃAB=![]() ЃЎ
ЃЎ

 ПьНнгЂгяжмжмСЗЯЕСаД№АИ
ПьНнгЂгяжмжмСЗЯЕСаД№АИ