题目内容
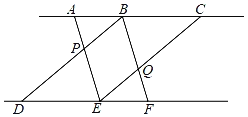
【题目】如图,从左向右依次摆放序号分别为1,2,3,…,n的小桶,其中任意相邻的四个小桶所放置的小球个数之和相等.
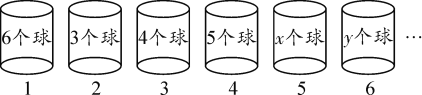
尝试 求x+y的值;
应用 若n=22,则这些小桶内所放置的小球个数之和是多少?
发现 用含k(k为正整数)的代数式表示装有“4个球”的小桶序号.
【答案】尝试:x+y=9;应用:99;发现:装有“4个球”的小桶序号为4k-1.
【解析】
尝试:根据“任意相邻的四个小桶所放置的小球个数之和相等”列出等式即可得到x+y的值;
应用:根据题意可分别求出x,y的值,可以发现以“6,3,4,5”为一组循环出现,故可求出n=22时,小桶内所放置的小球个数之和;
发现:根据规律,用含有k的代数式表示即可.
尝试:根据题意可得6+3+4+5=4+5+x+y,
∴x+y=9;
应用:∵6+3+4+5=3+4+5+x,
又∵x+y=9,
∴x=6,y=3,
∴小桶内所放置的小球数每四个一循环,
∵22÷4=52,
∴(6+3+4+5)×5+9=99
发现:装有“4个球”的小桶序号分别为3=4×1-1,7=4×2-1,11=4×3-1…,
∴装有“4个球”的小桶序号为4k-1.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
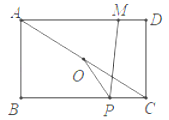
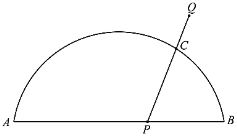
新课标快乐提优暑假作业陕西旅游出版社系列答案【题目】如图,![]() 是
是![]() 与弦
与弦![]() 所围成图形的外部的一定点,
所围成图形的外部的一定点,![]() 是弦
是弦![]() 上的一动点,连接
上的一动点,连接![]() 交
交![]() 于点
于点![]() .已知
.已知![]() ,设
,设![]() ,
,![]() 两点间的距离为
两点间的距离为![]() ,
,![]() ,
,![]() 两点间的距离为
两点间的距离为![]() ,
,![]() ,
,![]() 两点间的距离为
两点间的距离为![]() .
.
小石根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
(1)按照下表中自变量![]() 的值进行取点、画图、测量分别得到了
的值进行取点、画图、测量分别得到了![]() ,
,![]() 与
与![]() 的几组对应值:
的几组对应值:
| 0 | 1 | 2 | 3 | 4 | 5 | 5.40 | 6 |
| 4.63 | 3.89 | 2.61 | 2.15 | 1.79 | 1.63 | 0.95 | |
| 1.20 | 1.11 | 1.04 | 0.99 | 1.02 | 1.21 | 1.40 | 2.21 |
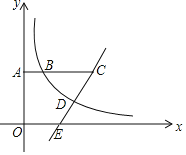
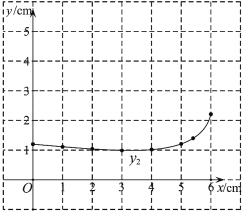
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() ,
,![]() 的图象;
的图象;
(3)结合函数图象,解决问题:当![]() 为
为![]() 的中点时,
的中点时,![]() 的长度约为______
的长度约为______![]() .
.