题目内容
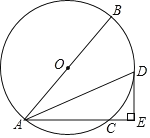
【题目】已知,A(0,8),B(4,0),直线y=﹣x沿x轴作平移运动,平移时交OA于D,交OB于C.
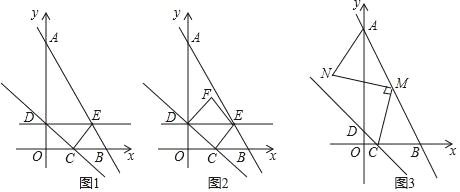
(1)当直线y=﹣x从点O出发以1单位长度/s的速度匀速沿x轴正方向平移,平移到达点B时结束运动,过点D作DE⊥y轴交AB于点E,连接CE,设运动时间为t(s).
①是否存在t值,使得△CDE是以CD为腰的等腰三角形?如果能,请直接写出相应的t值;如果不能,请说明理由.
②将△CDE沿DE翻折后得到△FDE,设△EDF与△ADE重叠部分的面积为y(单位长度的平方).求y关于t的函数关系式及相应的t的取值范围;
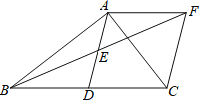
(2)若点M是AB的中点,将MC绕点M顺时针旋转90°得到MN,连接AN,请直接写出AN+MN的最小值.
【答案】(1)①t=2或t=﹣4![]() +8;②y=
+8;②y=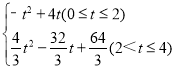 ;(2) AN+MN的最小值
;(2) AN+MN的最小值![]()
【解析】
(1)求出AB直线解析式,设出移动后的直线y=﹣x+t,当CD=CE时,当CD=DE时分别求出t的值;
(2)0≤t≤2时,y=S△EFD=﹣t2+4t;当2<t≤4时,DF所在直线解析式为y=x+t,得到DF⊥AB,作GP⊥DE,FQ⊥DE,由![]() ,
,![]() ,
,![]() ;
;
(3)N的运动轨迹在x=﹣2的线段上,当t=0时AN+MN最小.N(﹣2,6),AN+MN最小值![]() .
.
(1)设过A(0,8),B(4,0)两点的直线解析式为y=kx+b,
∴y=﹣2x+8,
①直线y=﹣x从点0出发以1单位长度/s的速度匀速沿x轴正方向平移,
此时函数解析式为y=﹣x+t,
∴D(0,t),E(t,8﹣2t),C(t,0),
当CD=CE时,
∴2t2=(8﹣3t)2+t2,
∴t=2或t=4,
当CD=DE时,
DE=|8﹣2t|,CD=![]() t,
t,
∴|8﹣2t|=![]() t,
t,
∴t=﹣4![]() +8,或t=8+4
+8,或t=8+4![]() ,
,
∵0≤t≤3,
∴t=2或t=﹣4![]() +8;
+8;
②∵△CDE沿DE翻折后得到△FDE,
∴F(t,2t),
当F在直线AB上时,t=2,
∴0≤t≤2时,
y=S△EFD=![]() ×(8﹣2t)t=﹣t2+4t,
×(8﹣2t)t=﹣t2+4t,
当2<t≤4时,
DF所在直线解析式为y=x+t,
∴DF⊥AB,
作GP⊥DE,FQ⊥DE,
∴FQ=t,DQ=t,GP=2PE,DE=8﹣2t,
∴![]() ,
,
∴![]() ,
,
![]() ;
;
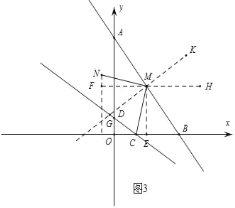
(3)如图3:过点M作ME⊥x轴,交x轴于E点;过点M作y轴垂线,过N做x轴垂线,相交于点F;过点M做AB直线的垂线,
∵∠NMC=∠NMG+∠CMG=90°,
∠GMB=∠GMC+∠CMB=90°,
∴∠NMG=∠CMB,
∵FH∥x轴,
∴∠CBA=∠HMB,
∵∠FMG=∠KMH,∠KMH+∠HMB=90°,∠BME+∠MBE=90°,
∴∠BME=∠KMH=∠FMG,
∴∠CME=∠NMF,
在Rt△NMF和Rt△CME中,MN=MC,∠CME=∠NMF,
∴Rt△NMF≌Rt△CME(AAS),
∴MF=ME,
∵点M是AB的中点,
∴M(2,4),
∴ME=MF=4,
∴N在NF所在直线上运动,
∴N点横坐标是﹣2,
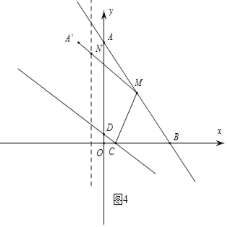
如图4:作A点关于直线x=﹣2的对称点A',连接A'M与x=﹣2交点为N,
此时AN+NM的值最小;
A'(﹣4,8),
∴A'M=![]() ;
;
∴AN+MN的最小值![]() ;
;

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案【题目】新冠疫情期间,某校开展线上教学,有“录播”和“直播”两种教学方式供学生选择其中一种.为分析该校学生线上学习情况,在接受这两种教学方式的学生中各随机抽取40人调查学习参与度,数据整理结果如表(数据分组包含左端值不包含右端值).
参与度 人数 方式 | 0.2~0.4 | 0.4~0.6 | 0.6~0.8 | 0.8~1 |
录播 | 4 | 16 | 12 | 8 |
直播 | 2 | 10 | 16 | 12 |
(1)你认为哪种教学方式学生的参与度更高?简要说明理由.
(2)从教学方式为“直播”的学生中任意抽取一位学生,估计该学生的参与度在0.8及以上的概率是多少?
(3)该校共有800名学生,选择“录播”和“直播”的人数之比为1:3,估计参与度在0.4以下的共有多少人?
【题目】在![]() 中,
中,![]() ,
,![]() ,在图中按下列步骤进行尺规作图:
,在图中按下列步骤进行尺规作图:
① | 以 |
② | 分别以 |
③ | 画射线 |
下列说法错误的是( )
A.![]() B.
B.![]()
C.![]() D.若
D.若![]() ,则
,则![]()