题目内容
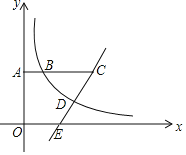
【题目】如图，已知点
，
，且点B在双曲线
上，在AB的延长线上取一点C，过点C的直线交双曲线于点D，交x轴正半轴于点E，且
，则线段CE长度的取值范围是
A. 
B. 
C. 
D. 
【答案】D
【解析】
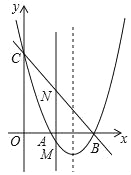
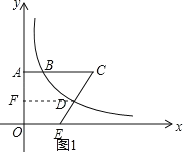
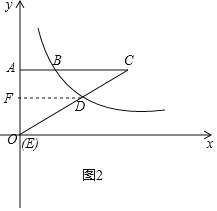
过D作DF⊥OA于F，得到DF是梯形的中位线，根据反比例函数图形上点的坐标特征求出D的坐标，当O与E重合时，如图2，由DF=8，根据三角形的中位线的性质得到AC，根据勾股定理求得CE，当CE⊥x轴时，CE=OA=6，于是求得结果．
过D作DF⊥OA于F．
∵点A（0，6），B（4，6），∴AB⊥y轴，AB=4，OA=6．
∵CD=DE，∴AF=OF=3．
∵点B在双曲线y
（k＞0）上，∴k=4×6=24，∴反比例函数的解析式为：y
．
∵过点C的直线交双曲线于点D，∴D点的纵坐标为3，代入y得：3，解得：x=8，∴D（8，3）．
当O与E重合时，如图2．
∵DF=8，∴AC=16．
∵OA=6，∴CE
；
当CE⊥x轴时，CE=OA=6，∴6≤CE≤2
．
故选D．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
