Question

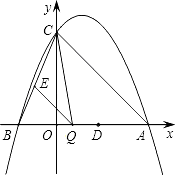
【题目】如图，以ABCO的顶点O为原点，边OC所在直线为x轴，建立平面直角坐标系，顶点A、C的坐标分别是（2，4）、（3，0），过点A的反比例函数的图象交BC于D，连接AD，则四边形AOCD的面积是 ．

Answer 1

【答案】9
【解析】解：∵四边形ABCD是平行四边形，A、C的坐标分别是（2，4）、（3，0），
∴点B的坐标为：（5，4），
把点A（2，4）代入反比例函数y=得：k=8，
∴反比例函数的解析式为：y=；
设直线BC的解析式为：y=kx+b，
把点B（5，4），C（3，0）代入得：，
解得：k=2，b=﹣6，
∴直线BC的解析式为：y=2x﹣6，
解方程组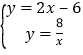 得：
，或 （不合题意，舍去），
∴点D的坐标为：（4，2），
即D为BC的中点，
∴△ABD的面积=平行四边形ABCD的面积，
∴四边形AOCD的面积=平行四边形ABCO的面积﹣△ABD的面积=3×4﹣×3×4=9；
所以答案是：9．
【考点精析】通过灵活运用比例系数k的几何意义和平行四边形的性质，掌握几何意义：表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积；平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分即可以解答此题．