Question

【题目】2015广州）如图，AC是⊙O的直径，点B在⊙O上，∠ACB=30°

（1）利用尺规作∠ABC的平分线BD，交AC于点E，交⊙O于点D，连接CD（保留作图痕迹，不写作法）
（2）在（1）所作的图形中，求△ABE与△CDE的面积之比．

Answer 1

【答案】
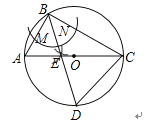
（1）

解：如图所示；

（2）

解：如图2，

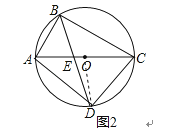
连接OD，设⊙O的半径为r，

∵∠BAE=∠CDE，

∠AEB=∠DEC，

∴△ABE∽△DCE，

在Rt△ACB中，∠ABC=90°，∠ACB=30°，

∴AB=AC=r，

∵∠ABD=∠ACD=45°，

∵OD=OC，

∴∠ABD=∠ACD=45°，

∴∠DOC=90°，

在Rt△ODC中，DC==r，

∴===．

【解析】（1）①以点B为圆心，以任意长为半径画弧，两弧交角ABC两边于点M，N；②分别以点M，N为圆心，以大于MN的长度为半径画弧，两弧交于一点；③作射线BE交AC与E，交⊙O于点D，则线段BD为△ABC的角平分线；
（2）连接OD，设⊙O的半径为r，证得△ABE∽△DCE，在Rt△ACB中，∠ABC=90°，∠ACB=30°，得到AB=AC=r，推出△ADC是等腰直角三角形，在Rt△ODC中，求得DC==r，于是问题可得．
【考点精析】根据题目的已知条件，利用圆周角定理的相关知识可以得到问题的答案，需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半．