题目内容
如图,⊙O的半径为l,等腰直角三角形ABC的顶点B的坐标为( ,0),∠CAB=90°,AC=AB,顶点A在⊙O上运动.
,0),∠CAB=90°,AC=AB,顶点A在⊙O上运动.
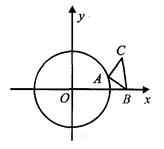
(1)当点A运动到x轴的负半轴上时,试判断直线BC与⊙O位置关系,并说明理由;
(2)当直线AB与⊙O相切时,求AB所在直线对应的函数关系式.
 ,0),∠CAB=90°,AC=AB,顶点A在⊙O上运动.
,0),∠CAB=90°,AC=AB,顶点A在⊙O上运动.
(1)当点A运动到x轴的负半轴上时,试判断直线BC与⊙O位置关系,并说明理由;
(2)当直线AB与⊙O相切时,求AB所在直线对应的函数关系式.
(1)直线BC与⊙O相切;(2) 当点A位于第一象限时, 过A、B两点的直线为y=-x+ ;当点A位于第四象限时, 过A、B两点的直线为y=x-
;当点A位于第四象限时, 过A、B两点的直线为y=x- .
.
 ;当点A位于第四象限时, 过A、B两点的直线为y=x-
;当点A位于第四象限时, 过A、B两点的直线为y=x- .
.试题分析:(1)直线BC与⊙O相切 1分
过点O作OM⊥BC于点M,
∴∠OBM=∠BOM="45°,"
∴OM=OB·sin45°=1
∴直线BC与⊙O相切
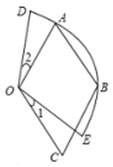
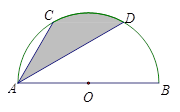
(2)①当点A位于第一象限时(如右图):

连接OA,并过点A作AE⊥OB于点E
∵直线AB与⊙O相切,∴∠OAB=90°,
又∵∠CAB=90°,
∴∠CAB+∠OAB=180°,
∴点O、A、C在同一条直线上
∴∠AOB=∠C=45°,
在Rt△OAE中,OE=AE=
 .
.点A的坐标为(
 ,
, )
) 过A、B两点的直线为y=-x+
 .
. ②当点A位于第四象限时(如右图):

点A的坐标为(
 ,-
,- )
) 过A、B两点的直线为y=x-
 .
.点评:本题考查直线与圆相切以及求直线所对应函数的解析式,解决此题考生对直线与圆相切的概念要熟悉,会求一次函数的解析式

练习册系列答案
相关题目


 .
.
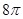 cm2,侧面展开图的圆心角为45°,则该圆锥的母线长为 cm.
cm2,侧面展开图的圆心角为45°,则该圆锥的母线长为 cm.