��Ŀ����
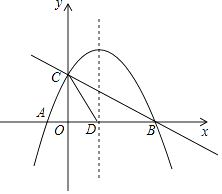
����Ŀ����ƽ��ֱ������ϵ�У�A(6��a)��B(b��0)��M(0��c)��P��Ϊy����һ���㣬��(b��2)2+|a��6|+![]() ��0��
��0��
(1)���B��M�����ꣻ
(2)��P�����߶�OM���˶�ʱ�������Ƿ����һ����PʹS��PAB��13�������ڣ������P���������AB�ij��ȣ��������ڣ���˵�����ɣ�
(3)����P���˶���ֱ��OM�ϵ��κ�λ��(��������O��M)����PAM����APB����PBO����֮���Ƿ���ij�̶ֹ���������ϵ������У���������ѧ֪ʶ�ҳ���֤�������û�У���˵�����ɣ�
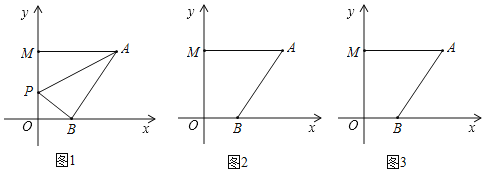
���𰸡���1��M��0��6����B��2��0����A��6��6������2��AB=2![]() ����3���ٵ���P���߶�OM��ʱ�����ۣ���APB+��PBO=��PAM�����ɼ��������ڵ���P��MO���ӳ�����ʱ�����ۣ���APB+��PBO=��PAM�����ɼ��������۵���P��OM���ӳ�����ʱ�����ۣ���PBO=��PAM+��APB�����ɼ�������
����3���ٵ���P���߶�OM��ʱ�����ۣ���APB+��PBO=��PAM�����ɼ��������ڵ���P��MO���ӳ�����ʱ�����ۣ���APB+��PBO=��PAM�����ɼ��������۵���P��OM���ӳ�����ʱ�����ۣ���PBO=��PAM+��APB�����ɼ�������
��������
��1�����÷Ǹ��������ʣ����a��b��c���ɽ�����⣻
��2����P��0��m��������S��PAB=S����AMOB-S��APM-S��PBO���������̼��ɽ�����⣻
��3�����������Σ��ֱ�ͼ�ν�����⼴����
��1���ߣ�b-2��2+|a-6|+![]() =0��
=0��
���ߣ�b-2��2����0��|a-6|��0��![]() ��0��
��0��
��a=6��b=2��c=6��
��M��0��6����B��2��0����A��6��6����
��2����P��0��m����
��S��PAB=13���ı���AMOB��ֱ�����Σ�
��![]() ��6+2��6-
��6+2��6-![]() m2-
m2-![]() ��6-m��6=13��
��6-m��6=13��
��m=![]() ��
��
��P��0��![]() ����
����
AB=![]() =2
=2![]() ��
��
��3������ͼ2-1�У�����P���߶�OM��ʱ�����ۣ���APB+��PBO=��PAM��
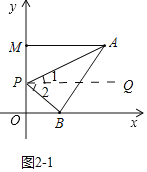
���ɣ���PQ��AM����PQ��AM��ON��
���1=��PAM����2=��PBO��
���1+��2=��PAM+��PBO��
����APB=��PAM+��PBO��
��APB+��PBO=��PAM��
����ͼ2-2����ʾ������P��MO���ӳ�����ʱ�����ۣ���APB+��PBO=��PAM��
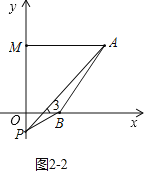
���ɣ���AM��OB��
���PAM=��3��
�ߡ�3=��APB+��PBO��
���APB+��PBO=��PAM��
����ͼ2-3�У�����P��OM���ӳ�����ʱ�����ۣ���PBO=��PAM+��APB��
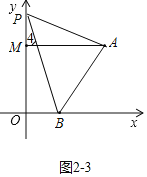
���ɣ���AM��OB��
���4=��PBO��
�ߡ�4=��PAM+��APB��
���PBO=��PAM+��APB��