题目内容
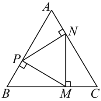
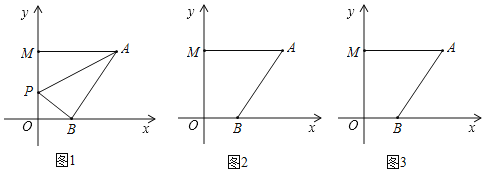
【题目】如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则 ![]() 的值等于 .
的值等于 . 
【答案】![]()
【解析】解:在正方形ABCD中,
∵∠ABD=∠CBD=45°,
∵四边形MNPQ和AEFG均为正方形,
∴∠BEF=∠AEF=90°,∠BMN=∠QMN=90°,
∴△BEF与△BMN是等腰直角三角形,
∴FE=BE=AE= ![]() AB,BM=MN=QM,
AB,BM=MN=QM,
同理DQ=MQ,
∴MN= ![]() BD=
BD= ![]() AB,
AB,
∴ ![]() =
= ![]() =
= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目