Question

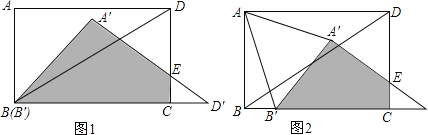
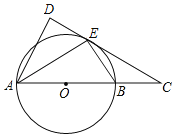
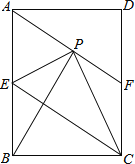
【题目】已知：如图，AB为⊙O的直径，AC与⊙O相切于点A，连接BC交圆于点D，过点D作⊙O的切线交AC于E．

（1）求证：AE＝CE

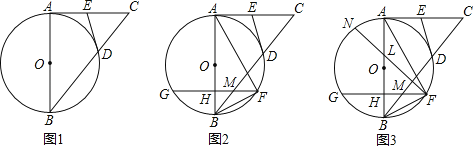
（2）如图，在弧BD上任取一点F连接AF，弦GF与AB交于H，与BC交于M，求证：∠FAB+∠FBM＝∠EDC．

（3）如图，在（2）的条件下，当GH＝FH，HM＝MF时，tan∠ABC＝，DE＝时，N为圆上一点，连接FN交AB于L，满足∠NFH+∠CAF＝∠AHG，求LN的长．

Answer 1

【答案】（1）详见解析；（2）详见解析；（3）

【解析】

（1）由直径所对的圆周角是直角，得∠ADC＝90°，由切线长定理得EA＝ED，再由等角的余角相等，得到∠C＝∠EDC，进而得证结论.

（2）由同角的余角相等，得到∠BAD＝∠C，再通过等量代换，角的加减进而得证结论.

（3）先由条件得到AB＝26，设HM＝FM＝a，GH＝HF＝2a，BH＝a，再由相交弦定理得到GHHF＝BHAH，从而求出FH，BH，AH，再由角的关系得到△HFL∽△HAF，从而求出HL，AL，BL，FL，再由相交弦定理得到LNLF＝ALBL，进而求出LN的长.

解：

（1）证明：如图1中，连接AD．

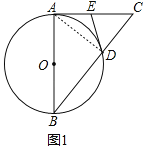
∵AB是直径，

∴∠ADB＝∠ADC＝90°，

∵EA、ED是⊙O的切线，

∴EA＝ED，

∴∠EAD＝∠EDA，

∵∠C+∠EAD＝90°，∠EDC+∠EDA＝90°，

∴∠C＝∠EDC，

∴ED＝EC，

∴AE＝EC．

（2）证明：如图2中，连接AD．

∵AC是切线，AB是直径，

∴∠BAC＝∠ADB＝90°，

∴∠BAD+∠CAD＝90°，∠CAD+∠C＝90°，

∴∠BAD＝∠C，

∵∠EDC＝∠C，

∴∠BAD＝∠EDC，

∵∠DBF＝∠DAF，

∴∠FBM+∠FAB＝∠FBM+∠DAF＝∠BAD，

∴∠FAB+∠FBM＝∠EDC．

（3）解：如图3中，

由（1）可知，DE＝AE＝EC，∵DE＝，

∴AC＝，

∵tan∠ABC＝＝，

∴,

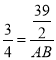∴AB＝26，

∵GH＝FH，HM＝FN，设HM＝FM＝a，GH＝HF＝2a，BH＝a，

∵GHHF＝BHAH，

∴4a2＝a（26﹣a），

∴a＝6，

∴FH＝12，BH＝8，AH＝18，

∵GH＝HF，

∴AB⊥GF，

∴∠AHG＝90°，

∵∠NFH+∠CAF＝∠AHG，

∴∠NFH+∠CAF＝90°，

∵∠NFH+∠HLF＝90°，

∴∠HLF＝∠CAF，

∵AC∥FG，

∴∠CAF＝∠AFH，

∴∠HLF＝∠AFH，

∵∠FHL＝∠AHF，

∴△HFL∽△HAF，

∴FH2＝HLHA，

∴122＝HL18，

∴HL＝8，

∴AL＝10，BL＝16，FL＝ ＝4，

∵LNLF＝ALBL，

∴4LN＝1016，

∴LN＝ .