题目内容
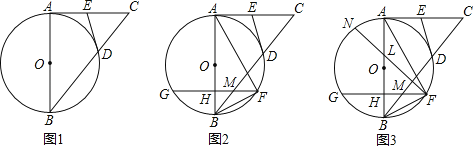
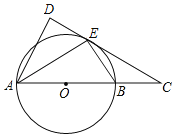
【题目】如图,AB是⊙O的直径,E是⊙O上一点,C在AB的延长线上,AD⊥CE交CE的延长线于点D,且AE平分∠DAC.
(1)求证:CD是⊙O的切线;
(2)若AB=6,∠ABE=60°,求AD的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)利用角平分线的性质得到∠OAE=∠DAE,再利用半径相等得∠AEO=∠OAE,等量代换即可推出OE∥AD,即可解题,(2)根据30°的三角函数值分别在Rt△ABE中,AE=AB·cos30°, 在Rt△ADE中,AD=cos30°×AE即可解题.
证明:如图,连接OE,
∵AE平分∠DAC,
∴∠OAE=∠DAE.
∵OA=OE,
∴∠AEO=∠OAE.
∴∠AEO=∠DAE.
∴OE∥AD.
∵DC⊥AC,
∴OE⊥DC.
∴CD是⊙O的切线.
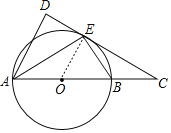
(2)解:∵AB是直径,
∴∠AEB=90°,∠ABE=60°.
∴∠EAB=30°,
在Rt△ABE中,AE=AB·cos30°=6×![]() =
=![]() ,
,
在Rt△ADE中,∠DAE=∠BAE=30°,
∴AD=cos30°×AE=![]() ×
×![]() =
=![]() .
.

练习册系列答案
相关题目