Question

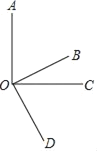
【题目】如图，射线OB、OC在∠AOD的内部，下列说法：

①若∠AOC＝∠BOD＝90°，则与∠BOC互余的角有2个；

②若∠AOD+∠BOC＝180°，则∠AOC+∠BOD＝180°；

③若OM、ON分别平分∠AOD，∠BOD，则∠MON＝∠AOB；

④若∠AOD＝150°、∠BOC＝30°，作∠AOP＝∠AOB、∠DOQ＝∠COD，则∠POQ＝90°

其中正确的有（　　）

A. 1个B. 2个C. 3个D. 4个

Answer 1

【答案】C

【解析】

根据余角和补角的定义和角平分线的定义进行计算即可得到结论．

④要分两种情况讨论. ∠AOP、∠DOQ是在内部还是外部.

解：①∵∠AOC＝∠BOD＝90°，

∴∠AOB+∠BOC＝∠COD+∠BOC＝90°，

∴与∠BOC互余的角有2个；正确；

②∵∠AOD+∠BOC＝∠AOB+∠BOC+∠COD+∠BCO＝∠AOC+∠BOD＝180°，

∴∠AOC+∠BOD＝180°；故正确；

③如图1，

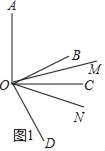
∵OM、ON分别平分∠AOD，∠BOD，

∴∠DOM＝ ∠AOD，∠DON＝∠BOD，

∴∠MON＝∠DOM﹣∠DON＝（∠AOD﹣∠BOD）＝∠AOB，故正确；

④如图2，

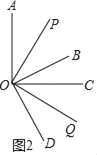
∵∠AOD＝150°、∠BOC＝30°，

∴∠AOB+∠COD＝150°﹣30°＝120°，

∵∠AOP＝∠AOB、∠DOQ＝∠COD，

∴∠AOP+∠DOQ＝（∠AOB+∠COD）＝60°，

∴∠POQ＝150°﹣60°＝90°，

如图3，

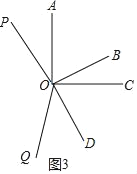
∵∠AOD＝150°、∠BOC＝30°，

∴∠AOB+∠COD＝150°﹣30°＝120°，

∵∠AOP＝∠AOB、∠DOQ＝∠COD，

∴∠AOP+∠DOQ＝（∠AOB+∠COD）＝60°，

∴∠POQ＝150°+60°＝210°，

综上所述，∠POQ＝90°或210°，故错误．

故选：C．