题目内容
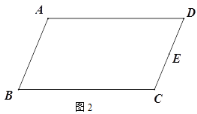
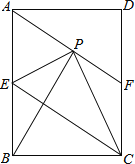
【题目】如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连接AP并延长AP交CD于F点,连接BP.
(1)求证:四边形AECF为平行四边形;
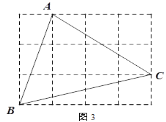
(2)若BC=![]() AB,判断△ABP的形状,并证明你的结论.
AB,判断△ABP的形状,并证明你的结论.
【答案】(1)见解析;(2)△APB是直角三角形.
【解析】
(1)由折叠的性质得到BE=PE,EC与PB垂直,根据E为AB中点,得到AE=EB=PE,利用三角形内一边上的中线等于这条边的一半的三角形为直角三角形,得到∠APB为90°,进而得到AF与EC平行,再由AE与FC平行,利用两对边平行的四边形为平行四边形即可得证;
(2)由(1)可得△APB是直角三角形.
解:(1)由折叠得到BE=PE,EC⊥PB,
∵E为AB的中点,
∴AE=EB=PE,
∴AP⊥BP,且EC⊥PB,
∴AF∥EC,
∵四边形ABCD是矩形,
∴AE∥FC,且AF∥EC,
∴四边形AECF为平行四边形;
(2)由(1)可知AP⊥BP
∴△APB是直角三角形

练习册系列答案
相关题目