Question

【题目】阅读材料，解决问题．

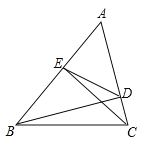
小聪在探索三角形中位线性质定理证明的过程中，得到了如下启示：一条线段经过另一线段的中点，则延长前者，并且长度相等，就能构造全等三角形．如图，D是△ABC的AC边的中点，E为AB上任一点，延长ED至F，使DF＝DE，连接CF，则可得△CFD≌△AED，从而把△ABC剪拼成面积相等的四边形BCFE．你能从小聪的反思中得到启示吗？

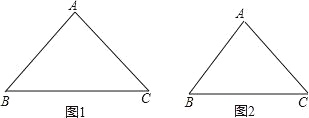
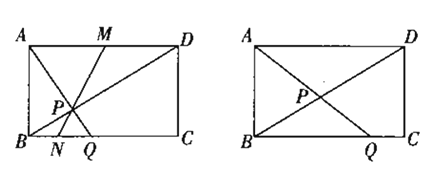
（1）如图1，已知△ABC，试着剪一刀，使得到的两块图形能拼成平行四边形．

①把剪切线和拼成的平行四边形画在图1上，并指出剪切线应符合的条件．

②思考并回答：要使上述剪拼得到的平行四边形成为矩形，△ABC的边或角应符合什么条件？菱形呢？正方形呢？（直接写出用符号表示的条件）

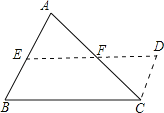
（2）如图2，已知锐角△ABC，试着剪两刀，使得到的三块图形能拼成矩形，把剪切线和拼成的矩形画在图2上，并指出剪切线应符合的条件．

Answer 1

【答案】（1）①见解析；②拼成矩形：∠B＝90°；拼成菱形：AB＝2BC；拼成正方形：∠B＝90°且AB＝2BC；（2）见解析

【解析】

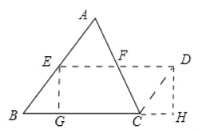
（1）①分别取AB，AC的中点E，F，延长EF至点D，使EF=FD，连接CD，因为两组边分别对应相等所以四边形BCDE是平行四边形，所以沿着EF剪出的两个图形能拼成平行四边形；

②当∠B=90°时，可根据有一个角是直角的平行四边形是矩形即可得到结论；
当AB=2BC时，根据有一组邻边相等的平行四边形是菱形可得到结论；
当∠B=90°且AB=2BC时，根据有一个角是直角的菱形是正方形即可得到结论．
（2）取△ABC的中位线EF，按第一问的方法先将其拼成一个平行四边形，再过点E作BC边的垂线EG，顺着EG剪下然后拼到点C处即可得到一个矩形．

解：（1）①如图：剪切线EF，E.F分别AB、AC的中点.

②如图，△ABC的边或角应符合的条件：

拼成矩形：∠B=90°

拼成菱形：AB=2BC

拼成正方形：∠B=90°且AB=2BC.

(2)如图，

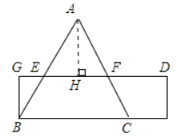
剪切线应符合的条件：剪切线EF是中位线、EG⊥BC(AH⊥EF).