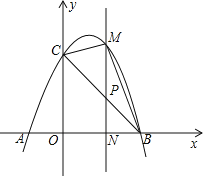
题目内容
【题目】已知抛物线y=x2+bx+c与x轴交于点A(﹣2,0)
(1)填空:c= ;(用含b的式子表示)
(2)b<4.
①求证:抛物线与x轴有两个交点;
②设抛物线与x轴的另一个交点为B,当线段AB上恰有5个整点(横坐标、纵坐标都是整数的点),求b的取值范围;
(3)平移抛物线,使其顶点P落在直线y=3x﹣2上,设抛物线与直线的另一个交点为Q,C在该直线下方的抛物线上,求△CPQ面积的最大值.
【答案】(1)2b﹣4;(2)①详见解析;②﹣1<b≤0;(3)△CPQ面积的最大值为![]() .
.
【解析】
(1)将点A的坐标代入抛物线的解析式求解即可;
(2)①由(1)可知抛物线的解析式为y=x2+bx+2b4,然后证明△>0即可;
②当点B在点A的右侧时,0≤![]() <
<![]() ;当点B在点A的左侧时,4.5<
;当点B在点A的左侧时,4.5<![]() ≤4,从而可求得b的取值范围;
≤4,从而可求得b的取值范围;
(3)以平移后抛物线的顶点为坐标原点建立坐标系,则在新坐标系内抛物线的解析式为y=x2,直线的解析式为y=3x.过点C作CD∥y轴,交直线于点D.设点C的坐标为(x,x2),则点D的坐标为(x,3x),则DC=3xx2,然后建立三角形的面积与x的函数关系式求解即可.
解:(1)将点A的坐标代入y=x2+bx+c得:4﹣2b+c=0,
∴c=2b﹣4,
故答案为:2b﹣4;
(2)①由(1)可知抛物线的解析式为y=x2+bx+2b﹣4,
∴△=b2﹣4(2b﹣4)=b2﹣8b+16=(b﹣4)2,
又∵b<4,
∴△>0,
∴抛物线与x轴有两个交点;
②当点B在点A的右侧时.
∵线段AB上恰有5个整点,
∴0≤![]() <
<![]() ,即0≤﹣
,即0≤﹣![]() b<
b<![]() ,
,
∴﹣1<b≤0;
当点B在点A的左侧时,
∵线段AB上恰有5个整点,
∴﹣4.5<![]() ≤﹣4,即﹣4.5<﹣
≤﹣4,即﹣4.5<﹣![]() b≤﹣4.
b≤﹣4.
∴8≤b<9.
解得:﹣1<b≤0或8≤b<9,
又∵b<4,
∴b的取值范围是:﹣1<b≤0;
(3)如图所示:
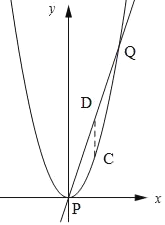
以平移后抛物线的顶点为坐标原点建立坐标系,则在新坐标系内抛物线的解析式为y=x2,直线的解析式为y=3x.
过点C作CD∥y轴,交直线于点D,
将y=3x代入y=x2得3x=x2,解得:x=0或x=3,
设点C的坐标为(x,x2),则点D的坐标为(x,3x),则DC=3x﹣x2,
∴△PQC的面积=![]() DC|xQ﹣xP|=
DC|xQ﹣xP|=![]() ×3×(3x﹣x2)=﹣
×3×(3x﹣x2)=﹣![]() x2+
x2+![]() =﹣
=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
∴△CPQ面积的最大值为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | -4 | -3 | -2 | -1 | 0 | 1 | … |
| … | 5 | 0 | -3 | -4 | -3 | m | … |
(1)m= ;
(2)在图中画出这个二次函数的图象;
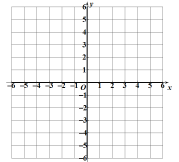
(3)当![]() 时,x的取值范围是 ;
时,x的取值范围是 ;
(4)当![]() 时,y的取值范围是 .
时,y的取值范围是 .