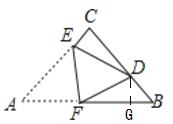
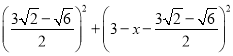题目内容
【题目】某报社为了了解市民“获取新闻的最主要途径”,开展了一次抽样调查,根据调查结果绘制了如下三种不完整的统计图表.
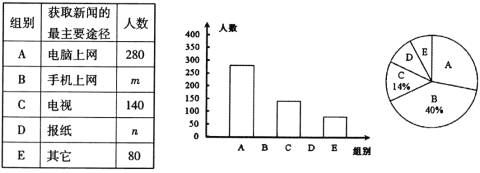
请根据图表信息解答下列问题:
(1)统计表中的![]() = ,
= ,![]() = ,并请补全条形统计图;
= ,并请补全条形统计图;
(2)扇形统计图中“![]() ”所对应的圆心角的度数是 ;
”所对应的圆心角的度数是 ;
(3)若该市约有100万人,请你估计其中将“电脑上网”和“手机上网”作为“获取新闻的最主要途径”的总人数.
【答案】(1)400,100;补图见解析;(2)36°;(3)68万人.
【解析】
(1)由C组的人数除以占的百分比,得出调查总人数,进而确定出B组与D组的人数,得到m与n的值,从而补全条形统计图;
(2)由D组所占的百分比,乘以360°即可得到结果;
(3)用该市总人数乘以A、B两组所占百分比的和即可得到结论.
(1)调查总人数为:140÷14%=1000(人),
m=1000×40%=400,
n=1000-280-400-140-80=100.
条形图补充如图所示:
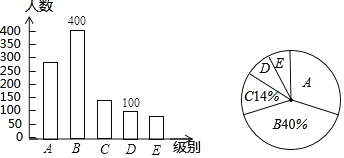
(2)扇形统计图中“D”所对应的圆心角的度数是![]() ×360°=36°;
×360°=36°;
故答案为:36°;
(3)![]() ×100=68(万人),
×100=68(万人),
答:估计其中将“电脑上网”和“手机上网”作为“获取新闻的最主要途径”的总人数为68万人.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】“2018东台西溪半程马拉松”的赛事共有两项:A、“半程马拉松”、 B、“欢乐跑”。小明参加了该项赛事的志愿者服务工作, 组委会随机将志愿者分配到两个项目组.
(1)小明被分配到“半程马拉松”项目组的概率为________.
(2)为估算本次赛事参加“半程马拉松”的人数,小明对部分参赛选手作如下调查:
调查总人数 | 20 | 50 | 100 | 200 | 500 |
参加“半程马拉松”人数 | 15 | 33 | 72 | 139 | 356 |
参加“半程马拉松”频率 | 0.750 | 0.660 | 0.720 | 0.695 | 0.712 |
①请估算本次赛事参加“半程马拉松”人数的概率为_______.(精确到0.1)
②若本次参赛选手大约有3000人,请你估计参加“半程马拉松”的人数是多少?