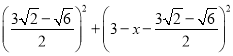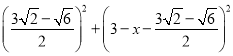题目内容
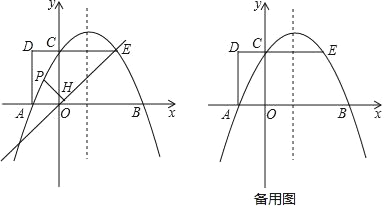
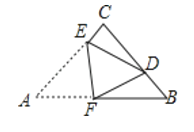
【题目】如图,已知一次函数y=![]() x﹣3与反比例函数y=
x﹣3与反比例函数y=![]() 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.
(1)求反比例函数的表达式;
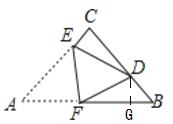
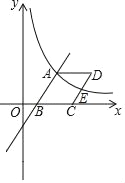
(2)将线段AB沿x轴向右平移5个单位到DC,设DC与双曲线交于点E,求点E到x轴的距离.
【答案】(1)反比例函数的解析式为y=![]() ;(2)点E到x轴的距离为
;(2)点E到x轴的距离为![]() .
.
【解析】分析:(1)把点A(4,n)代入一次函数y=![]() x-3,得到n的值为3;再把点A(4,3)代入反比例函数y=
x-3,得到n的值为3;再把点A(4,3)代入反比例函数y=![]() ,得到k的值为12,即可写出方比例函数的解析式;
,得到k的值为12,即可写出方比例函数的解析式;
(2)设E(![]() ,m),根据tan∠ECx=tan∠ABC构建方程即可解决问题.
,m),根据tan∠ECx=tan∠ABC构建方程即可解决问题.
详解:(1)把点A(4,n)代入一次函数y=![]() x﹣3,
x﹣3,
可得n=![]() ×4﹣3=3;
×4﹣3=3;
把点A(4,3)代入反比例函数y=![]() ,
,
可得3=![]() ,
,
解得k=12.
∴反比例函数的解析式为y=![]() .
.
(2)设E(![]() ,m),
,m),
一次函数y=![]() x-3与x轴交点B(2,0),
x-3与x轴交点B(2,0),
BC=AD=5,
∴OC=7,
∵tan∠ECx=tan∠ABC,
∴![]() =
=![]() ,
,
解得m=![]() (负根已经舍弃),
(负根已经舍弃),
∴点E到x轴的距离为![]() .
.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
【题目】“2018东台西溪半程马拉松”的赛事共有两项:A、“半程马拉松”、 B、“欢乐跑”。小明参加了该项赛事的志愿者服务工作, 组委会随机将志愿者分配到两个项目组.
(1)小明被分配到“半程马拉松”项目组的概率为________.
(2)为估算本次赛事参加“半程马拉松”的人数,小明对部分参赛选手作如下调查:
调查总人数 | 20 | 50 | 100 | 200 | 500 |
参加“半程马拉松”人数 | 15 | 33 | 72 | 139 | 356 |
参加“半程马拉松”频率 | 0.750 | 0.660 | 0.720 | 0.695 | 0.712 |
①请估算本次赛事参加“半程马拉松”人数的概率为_______.(精确到0.1)
②若本次参赛选手大约有3000人,请你估计参加“半程马拉松”的人数是多少?