题目内容
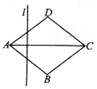
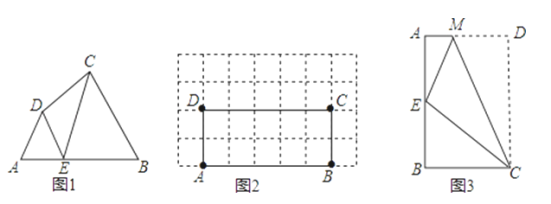
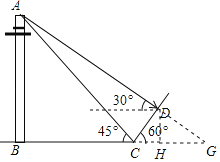
【题目】某校王老师组织九(1)班同学开展数学活动,某天带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A的仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高AB.(结果用根号表示)
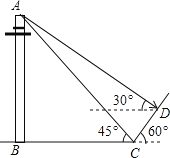
【答案】电线杆的高为4(![]() +1)m.
+1)m.
【解析】
根据直角三角形中边角关系,延长AD交BC延长线与点G,作DH⊥BG于H,构建直角三角形,由三角函数求出CH和DH的长度,得出CG,设AB为xm,根据正切的定义求出BG,得出方程,解这个方程即可.
延长AD交BC的延长线于G,作DH⊥BG于H,
在Rt△DHC中,
∠DCH=60°,CD=4,
则CH=CDcos∠DCH=4×cos60°=2,
DH=CDsin∠DCH=4×sin60°=![]() ,
,
∵DH⊥BG,∠G=30°,
∴HG=![]() =
=![]() =6,
=6,
∴CG=CH+HG=2+6=8,
设AB=xm,
∵AB⊥BG,∠G=30°,∠BCA=45°,
∴BC=x,
BG=![]() =
=![]() x,
x,
∵BG﹣BC=CG,
∴![]() x﹣x=8,
x﹣x=8,
解得:x=![]() =4(
=4(![]() +1)(m)
+1)(m)
答:电线杆的高为x=4(![]() +1)m.
+1)m.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
【题目】成都市某公司自主设计了一款可控温杯,每个生产成本为16元,投放市场进行了试销.经过调查得到每月销售量y(万个)与销售单价x(元/个)之间关系是一次函数的关系,部分数据如下:
销售单价x(元/个) | … | 20 | 25 | 30 | 35 | … |
每月销售量y(万个) | … | 60 | 50 | 40 | 30 | … |
(1)求y与x之间的函数关系;
(2)该公司既要获得一定利润,又要符合相关部门规定(一件产品的利润率不得高于50%)请你帮助分析,公司销售单价定为多少时可获利最大?并求出最大利润.