题目内容
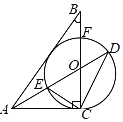
【题目】如图,在△ABC中,∠ACB=90°,AO平分∠BAC,交BC于点O.以O为圆心,OC为半径作⊙O,分别交AO,BC于点E,F.
(1)求证:AB是⊙O的切线;
(2)延长AO交⊙O于点D,连接CD,若AD=2AC,求tanD的值;
(3)在(2)的条件下,设⊙O的半径为3,求BC的长.
【答案】(1)证明见解析;(2)tan∠D=![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据题意过点O作OM⊥AB,由角平分线到性质可得OC=OM,即可证AB是⊙O的切线;
(2)由题意证明△ACE∽△ADC,可得![]() ,以此进行分析即可得出结论.
,以此进行分析即可得出结论.
(3)根据题意由相似三角形的性质可得![]() ,即可求AD=8,AC=4=AM,通过证明△OBM∽△ABC,可得
,即可求AD=8,AC=4=AM,通过证明△OBM∽△ABC,可得![]() ,可得关于OB,BM的方程组,即可求BM的长,即可求AB和BC的长.
,可得关于OB,BM的方程组,即可求BM的长,即可求AB和BC的长.
证明:(1)如图,过点O作OM⊥AB,
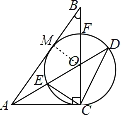
∵AO平分∠BAC,OM⊥AB,∠ACB=90°,
∴OC=OM,
∴OM为⊙O半径,且OM⊥AB,
∴AB是⊙O切线.
(2)解:∵DE是⊙O的直径,
∴∠DCE=90°,
∵∠ACB=90°,
∴∠DCE=∠ACB,
∴∠DCO=∠ACE,
∵OC=OD,
∴∠D=∠DCO,
∴∠ACE=∠D,且∠A=∠A,
∴△ACE∽△ADC,
∴![]() ,
,
∵AD=2AC,
∴tan∠D=![]() ;
;
(3)∵△ACE∽△ADC,
∴![]() ,
,
∴AC2=AD(AD﹣6),且2AC=AD,
∴AD=8,
∴AC=4,
∵AO=AO,OC=OM,
∴Rt△AOM≌Rt△AOC(HL),
∴AM=AC=4,
∵∠B=∠B,∠OMB=∠ACB=90°
∴△OBM∽△ABC,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴BM=![]() ,
,
∴AB=4+![]() =
=![]() ,
,
∴BC=![]() =
=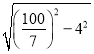 =
=![]() .
.

练习册系列答案
相关题目