ΧβΡΩΡΎ»ί
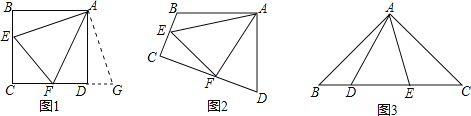
ΓΨΧβΡΩΓΩ‘ΡΕΝάμΫβΘΚ»γΆΦ1Θ§‘ΎΥΡ±Ώ–ΈABCDΒΡ±ΏAB…œ»Έ»Γ“ΜΒψEΘ®ΒψE≤Μ”κAΓΔB÷ΊΚœΘ©Θ§Ζ÷±πΝ§Ϋ”EDΓΔECΘ§Ω…“‘Α―ΥΡ±Ώ–ΈABCDΖ÷≥…»ΐΗω»ΐΫ«–ΈΘ§»γΙϊΤδ÷–”–ΝΫΗω»ΐΫ«–ΈœύΥΤΘ§Έ“Ο«ΨΆΑ―EΫ–ΉωΥΡ±Ώ–ΈABCDΒΡ±ΏAB…œΒΡΓΑœύΥΤΒψΓ±ΘΚ»γΙϊ’β»ΐΗω»ΐΫ«–ΈΕΦœύΥΤΘ§Έ“Ο«ΨΆΑ―EΫ–ΉωΥΡ±Ώ–ΈABCDΒΡ±ΏAB…œΒΡΓΑ«ΩœύΥΤΒψΓ±Θ°ΫβΨωΈ ΧβΘΚ
Θ®1Θ©»γΆΦ1Θ§ΓœA=ΓœB=ΓœDEC=45ΓψΘ§ ‘≈–ΕœΒψE «Ζώ «ΥΡ±Ώ–ΈABCDΒΡ±ΏAB…œΒΡœύΥΤΒψΘ§≤ΔΥΒΟςάμ”…ΘΜ
Θ®2Θ©»γΆΦ2Θ§‘ΎΨΊ–ΈABCD÷–Θ§AΓΔBΓΔCΓΔDΥΡΒψΨυ‘Ύ’ΐΖΫ–ΈΆχΗώΘ®ΆχΗώ÷–ΟΩΗω–Γ’ΐΖΫ–ΈΒΡ±Ώ≥ΛΈΣ1Θ©ΒΡΗώΒψΘ®Φ¥ΟΩΗω–Γ’ΐΖΫ–ΈΒΡΕΞΒψΘ©…œΘ§ ‘‘ΎΆΦΔΎ÷–Μ≠≥ωΨΊ–ΈABCDΒΡ±ΏAB…œΒΡ«ΩœύΥΤΒψΘΜΓΓΓΓ
Θ®3Θ©»γΆΦ3Θ§ΫΪΨΊ–ΈABCD―ΊCM’έΒΰΘ§ ΙΒψD¬δ‘ΎAB±Ώ…œΒΡΒψE¥ΠΘ§»τΒψE«ΓΚΟ «ΥΡ±Ώ–ΈABCMΒΡ±ΏAB…œΒΡ“ΜΗω«ΩœύΥΤΒψΘ§ ‘ΧΫΨΩAB”κBCΒΡ ΐΝΩΙΊœΒΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ΒψE «ΥΡ±Ώ–ΈABCDΒΡ±ΏAB…œΒΡœύΥΤΒψΘ§άμ”…ΦϊΫβΈωΘΜΘ®2Θ©ΦϊΫβΈωΘΜΘ®3Θ©![]() =
=![]()
ΓΨΫβΈωΓΩ
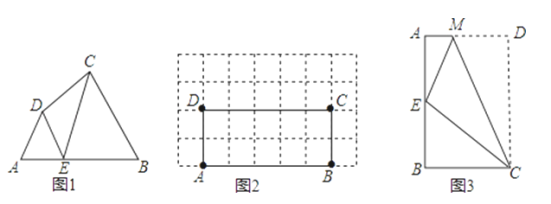
Θ®1Θ©“Σ÷ΛΟςΒψE «ΥΡ±Ώ–ΈABCDΒΡAB±Ώ…œΒΡœύΥΤΒψΘ§÷Μ“Σ÷ΛΟς”–“ΜΉι»ΐΫ«–ΈœύΥΤΨΆ––Θ§Κή»ί“Ή÷ΛΟςΓςADEΓΉΓςBECΘ§Υυ“‘Έ ΧβΒΟΫβΘ°
Θ®2Θ©“‘CDΈΣ÷±ΨΕΜ≠ΜΓΘ§»ΓΗΟΜΓ”κABΒΡ“ΜΗωΫΜΒψΦ¥ΈΣΥυ«σΘ°
Θ®3Θ©”…ΒψE «ΨΊ–ΈABCDΒΡAB±Ώ…œΒΡ“ΜΗω«ΩœύΥΤΒψΘ§ΒΟΓςAEMΓΉΓςBCEΓΉΓςECMΘ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡΕ‘”ΠΫ«œύΒ»Θ§Ω…«σΒΟΓœBCE=![]() ΓœBCD=30ΓψΘ§άϊ”ΟΚ§30ΓψΫ«ΒΡ÷±Ϋ«»ΐΫ«–Έ–‘÷ Ω…ΒΟBE”κABΘ§BC±Ώ÷°ΦδΒΡ ΐΝΩΙΊœΒΘ§¥”ΕχΩ…«σ≥ωAB”κBC±Ώ÷°ΦδΒΡ ΐΝΩΙΊœΒΘ°
ΓœBCD=30ΓψΘ§άϊ”ΟΚ§30ΓψΫ«ΒΡ÷±Ϋ«»ΐΫ«–Έ–‘÷ Ω…ΒΟBE”κABΘ§BC±Ώ÷°ΦδΒΡ ΐΝΩΙΊœΒΘ§¥”ΕχΩ…«σ≥ωAB”κBC±Ώ÷°ΦδΒΡ ΐΝΩΙΊœΒΘ°
Θ®1Θ©ΓΏΓœA=ΓœDEC=45Γψ
ΓύΓœADE+ΓœAED=135ΓψΘ§ΓœBEC+ΓœAED=135ΓψΘ§
ΓύΓœADE=ΓœBECΘ§
”÷ΓΏΓœA=ΓœBΘ§
ΓύΓςADEΓΉΓςBECΘ§
ΓύΒψE «ΥΡ±Ώ–ΈABCDΒΡ±ΏAB…œΒΡœύΥΤΒψΘΜ
Θ®2Θ©»γΆΦ÷–Υυ ΨΒΡΒψEΚΆΒψFΈΣAB…œΒΡ«ΩœύΥΤΒψΘΜ
Θ®3Θ©ΓΏΒψE «ΥΡ±Ώ–ΈABCMΒΡ±ΏAB…œΒΡ“ΜΗω«ΩœύΥΤΒψΘ§
ΓύΓςAEMΓΉΓςBCEΓΉΓςECMΘ§
ΓύΓœBCE=ΓœECM=ΓœAEMΘ§
”…’έΒΰΩ…÷ΣΘΚΓςECMΓ’ΓςDCMΘ§
ΓύΓœECM=ΓœDCMΘ§CE=CDΘ§
ΓύΓœBCE=![]() ΓœBCD=30ΓψΘ§CE=ABΘ§
ΓœBCD=30ΓψΘ§CE=ABΘ§
‘ΎRtΓςBCE÷–Θ§cosΓœBCE=![]() Θ§
Θ§
Γύ![]() =
=![]() Θ§
Θ§
Γύ![]() =
=![]() Θ°
Θ°

 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ