题目内容
【题目】如图,已知正方形ABCD,从顶点A引两条射线分别交BC,CD于点E,F,且∠EAF=45°.
求证:BE+DF=EF.

【答案】证明见解析
【解析】
延长CD到G,使DG=BE,利用“边角边”证明△ABE和△ADG全等,根据全等三角形对应边相等可得AG=AE,全等三角形对应角相等可得∠DAG=∠BAE,然后求出∠EAF=∠GAF,再利用“边角边”证明△AEF和△AGF全等,根据全等三角形对应边相等可得EF=GF,然后结合图形整理即可得证.
证明:延长CD到点G,使DG=BE,连接AG.
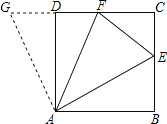
在正方形ABCD中,AB=AD,∠B=∠ADC=90°,
所以∠ADG=∠B.
在△ABE和△ADG中,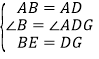 ,
,
所以△ABE≌△ADG(SAS).
所以AE=AG,∠BAE=∠DAG.
因为∠EAF=45°,
所以∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=90°-45°=45°.
所以∠EAF=∠GAF,
在△AEF和△AGF中,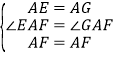 ,
,
所以△AEF≌△AGF(SAS).
所以EF=GF.
所以EF=GF=DG+DF=BE+DF,
即BE+DF=EF.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目