题目内容
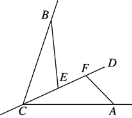
【题目】如图,在△ABC 中,∠C=90° 
(1)利用尺规作∠B 的角平分线交AC于D,以BD为直径作⊙O交AB于E(保留作图痕迹,不写作法);
(2)综合应用:在(1)的条件下,连接DE ①求证:CD=DE;
②若sinA= ![]() ,AC=6,求AD.
,AC=6,求AD.
【答案】
(1)解: 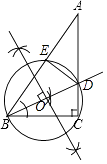
(2)解:①∵BD为⊙O的直径;
∴∠BED=90°,
又∵∠C=90°;
∴DE⊥AB,DC⊥BC;
又∵BD平分∠ABC;
∴DE=DC;
②在Rt△ADE中,sinA= ![]()
∵sinA= ![]()
∴ ![]() =
= ![]()
设DC=DE=3x,AD=5x
∵AC=AD+DC
∴3x+5x=6x= ![]()
AD=5x=5× ![]() =
= ![]()
【解析】(1)根据题意作出图形即可;(2)有BD为⊙O的直径;得到∠BED=90°,根据角平分线的性质即可得到结论;(3)解直角三角形即可得到结论.
【考点精析】掌握圆周角定理和解直角三角形是解答本题的根本,需要知道顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).

练习册系列答案
相关题目