题目内容
【题目】定义,我们把对角线互相垂直的四边形叫做垂美四边形.
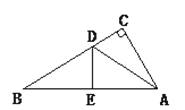
概念理解:如图②,在四边形ABCD中,如果AB=AD,CB=CD,那么四边形ABCD是垂美四边形吗?请说明理由.
性质探究:如图①,垂美四边形ABCD两组对边AB、CD与BC、AD之间有怎样的数量关系?写出你的猜想,并给出证明.
问题解决:如图③,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG 和正方形ABDE,连结CE、BG、GE.若AC=2,AB=5,则①求证:△AGB≌△ACE;
②GE= .

【答案】(1)是;(2)AB2+CD2=BC2+AD2;(3)①证明见解析;②![]() .
.
【解析】
概念理解:根据垂直平分线的判定定理证明即可;
性质探究:根据垂直的定义和勾股定理解答即可;
问题解决:根据垂美四边形的性质、勾股定理、结合(2)的结论计算即可.
概念理解:四边形ABCD是垂美四边形.理由如下:
∵AB=AD,∴点A在线段BD的垂直平分线上.
∵CB=CD,∴点C在线段BD的垂直平分线上,∴直线AC是线段BD的垂直平分线,∴AC⊥BD,即四边形ABCD是垂美四边形;
性质探究:AD2+BC2=AB2+CD2.理由如下:
如图2,已知四边形ABCD中,AC⊥BD,垂足为E.
∵AC⊥BD,∴∠AED=∠AEB=∠BEC=∠CED=90°,由勾股定理得:AD2+BC2=AE2+DE2+BE2+CE2,AB2+CD2=AE2+BE2+CE2+DE2,∴AD2+BC2=AB2+CD2;
问题解决:①连接CG、BE,如图3所示:
∵∠CAG=∠BAE=90°,∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE.
在△GAB和△CAE中,∵AG=AC,∠GAB=∠CAE,AB=AE,∴△AGB≌△ACE(SAS);
②∵△AGB≌△ACE,∴∠ABG=∠AEC.
又∵∠AEC+∠AME=90°,∴∠ABG+∠AME=90°,即CE⊥BG,∴四边形CGEB是垂美四边形,由(2)得:CG2+BE2=CB2+GE2.
∵AC=2,AB=5,∴BC=![]() ,CG=2
,CG=2![]() ,BE=5
,BE=5![]() ,∴GE2=CG2+BE2﹣CB2=37,∴GE=
,∴GE2=CG2+BE2﹣CB2=37,∴GE=![]() .
.
故答案为:![]() .
.