题目内容
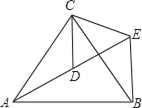
【题目】已知正方形ABCD中,BC=3,点E、F分别是CB、CD延长线上的点,DF=BE,连接AE、AF,过点A作AH⊥ED于H点. 
(1)求证:△ADF≌△ABE;
(2)若BE=1,求tan∠AED的值.
【答案】
(1)解:正方形ABCD中,
∵AD=AB,∠ADC=∠ABC=90°,
∴∠ADF=∠ABE=90°,
在△ADF与△ABE中,
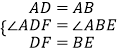 ,
,
∴△ADF≌△ABE
(2)解:过点A作AH⊥DE于点H,
在Rt△ABE中,∵AB=BC=3,
∵BE=1,
∴AE= ![]() ,ED=
,ED= ![]() =5,
=5,
∵S△AED= ![]() AD×BA=
AD×BA= ![]() ,
,
S△ADE= ![]() ED×AH=
ED×AH= ![]() ,
,
解出AH=1.8,
在Rt△AHE中,EH=2.6,
∴tan∠AED= ![]() .
.
【解析】(1)根据辅助线的性质得到AD=AB,∠ADC=∠ABC=90°,由邻补角的定义得到∠ADF=∠ABE=90°,于是得到结论;(2)过点A作AH⊥DE于点H,根据勾股定理得到AE= ![]() ,ED=
,ED= ![]() =5,根据三角形的面积S△AED=
=5,根据三角形的面积S△AED= ![]() AD×BA=
AD×BA= ![]() ,S△ADE=
,S△ADE= ![]() ED×AH=
ED×AH= ![]() ,求得AH=1.8,由三角函数的定义即可得到结论.本题考查了正方形的性质,全等三角形的判定和性质,三角形的面积倒计时,勾股定理,熟练掌握正方形的性质是解题的关键.
,求得AH=1.8,由三角函数的定义即可得到结论.本题考查了正方形的性质,全等三角形的判定和性质,三角形的面积倒计时,勾股定理,熟练掌握正方形的性质是解题的关键.

练习册系列答案
相关题目