��Ŀ����
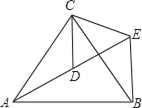
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�Rt��ABC����������ֱ���A����8��3����B����4��0����C����4��3������ABC=���㣮������y= ![]() x2+bx+c������C���ҶԳ���Ϊx=��
x2+bx+c������C���ҶԳ���Ϊx=�� ![]() ������y�ύ�ڵ�G��
������y�ύ�ڵ�G��
��1���������ߵĽ���ʽ����G�����ꣻ
��2����Rt��ABC��x������ƽ��m����λ��ʹB���Ƶ���E��Ȼ���������Ƶ�E˳ʱ����ת����õ���DEF������Fǡ�������������ϣ�
����m��ֵ��
������CG��x���ڵ�H������FG����B��BP��FG����CG�ڵ�P����֤��PH=GH��
���𰸡�
��1��
�⣺��������ã� 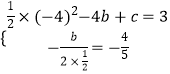
��ã� 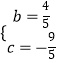
�������ߵĽ���ʽΪ��y= ![]() x2+
x2+ ![]() x-
x- ![]() ����G��0����
����G��0���� ![]() ��
��
��2��
�⣺�ٹ�F��FM��y�ᣬ��DE��M����y����N��
�������֪��AC=4��BC=3����AB=5��FM= ![]() ��
��
��Rt��ABC��x������ƽ��m����λ��ʹB���Ƶ���E��
��E����4+m��0����OE=MN=4��m��FN= ![]() ����4��m��=m��
����4��m��=m�� ![]() ��
��
��Rt��FME�У��ɹ��ɶ����ã�EM= ![]() =
= ![]() ��
��
��F��m�� ![]() ��
�� ![]() ����
����
��F�������ϣ�
�� ![]() =
= ![]() ��m��
��m�� ![]() ��2+
��2+ ![]() ��m��
��m�� ![]() ����
���� ![]() ��
��
5m2��8m��36=0��
m1=��2���ᣩ�� ![]() ��
��
�������FG�Ľ���ʽΪ��y= ![]() x��
x�� ![]() ��
��
CG����ʽΪ��y=�� ![]() x��
x�� ![]() ��
��
�� ![]() x��
x�� ![]() =0��x=1����Q��1��0����
=0��x=1����Q��1��0����
�� ![]() x��
x�� ![]() =0��x=��1.5����H����1.5��0����
=0��x=��1.5����H����1.5��0����
��BH=4��1.5=2.5��HQ=1.5+1=2.5��
��BH=QH��
��BP��FG��
���PBH=��GQH����BPH=��QGH��
���BPH�ա�QGH��
��PH=GH��
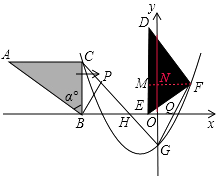
����������1���ѵ�C�������y= ![]() x2+bx+c��һ���̣����öԳ��ṫʽ����һ���̣���ɷ������������ʽ�������G������ꣻ��2�����������ߣ�����ֱ�ǡ�DEFб���ϵĸ�FM������ֱ�������ε������Ⱥ��ɶ����ɱ�ʾF�����꣬���ݵ�F���������ϣ��з������m��ֵ����F���G��������֪���������ֱ��FG�ķ��̣���ôFG��x��Ľ������꣨��ΪQ������֪����C��������֪��CG�ķ���Ҳ�����������ôH������������������֤����BPH�͡�MGHȫ�ȣ������Ƕ��κ������ۺ��⣬�����˴���ϵ�������������κ�����һ�κ������Ľ���ʽ�����ý���ʽ���������ύ�����꣬�����������б���ϵĸ�������ȫ�ȵ����ʵȣ��ۺ��Խ�ǿ�����ѶȲ�����һ���������п�ѹ���⣮
x2+bx+c��һ���̣����öԳ��ṫʽ����һ���̣���ɷ������������ʽ�������G������ꣻ��2�����������ߣ�����ֱ�ǡ�DEFб���ϵĸ�FM������ֱ�������ε������Ⱥ��ɶ����ɱ�ʾF�����꣬���ݵ�F���������ϣ��з������m��ֵ����F���G��������֪���������ֱ��FG�ķ��̣���ôFG��x��Ľ������꣨��ΪQ������֪����C��������֪��CG�ķ���Ҳ�����������ôH������������������֤����BPH�͡�MGHȫ�ȣ������Ƕ��κ������ۺ��⣬�����˴���ϵ�������������κ�����һ�κ������Ľ���ʽ�����ý���ʽ���������ύ�����꣬�����������б���ϵĸ�������ȫ�ȵ����ʵȣ��ۺ��Խ�ǿ�����ѶȲ�����һ���������п�ѹ���⣮
�����㾫����������Ҫ������ȷ��һ�κ����ı���ʽ��ȫ�������ε����ʵ����֪ʶ�㣬��Ҫ����ȷ��һ��һ�κ�������Ҫȷ��һ�κ�������ʽy=kx+b��k������0���еij���k��b�������������һ�㷽���Ǵ���ϵ������ȫ�������εĶ�Ӧ�����; ȫ�������εĶ�Ӧ����Ȳ�����ȷ�����⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ����������������ͨ�����ֻ�ͨ�����ѵ��������壬Ŀǰ��ijͨ�Ź�˾�Ƴ������Ż����Щ����������ײ͡��������߿ɸ���ʵ��������ɶ���ÿ����������������ͨ��ʱ�䣬�����ն��ߵĽ����ʷѱ�����ͨ�ŷѣ��±��������������Ľ��ݶ��۱���
�������ݶ��۱� | |
ʹ�÷�Χ | ���ݵ��ۣ�Ԫ/MB�� |
1��100MB | a |
101��500MB | 0.07 |
501��20GB | b |
�������ݶ��۱� | |
ʹ�÷�Χ | �����ʷѣ�Ԫ/���ӣ� |
1��500���� | 0.15 |
501��1000���� | 0.12 |
1001��2000���� | m |
��С��ʾ�����ݶ����շѼ��㷽������600��������ͨ����=0.15��500+0.12����600��500��=87Ԫ��
��1��������600MB��������������48Ԫ���Ҷ�����2GB��������������120.4Ԫ����a��b��ֵ����ע��1GB=1024MB��
��2�����ײͷ���Ϊ199Ԫ�����к�600MB���������������ײͷ���Ϊ244.2Ԫ�����а���1GB�������������˾������˳���1000���ӵ�ÿ��ͨ��ʱ�䣬���ұ�������ͨ��ʱ��ȼ�300���ӣ���m��ֵ��
����Ŀ��2016��ǭ�����ݽ�������֯ȫ����Сѧ���μ�ȫʡ��ȫ֪ʶ���羺������ȫ�ݰ�ȫ֪ʶ����������ͨ�����ϲ�ѯ��ijУһ�������ζԱ���ɼ����ɼ�ȡ����������100�֣�����ͳ�Ʒ��������Ƴ�����Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ���������ͼ���ṩ����Ϣ������������⣺ 
��1��Ƶ���ֲ�����a= �� b= �� c=
��2����ȫƵ���ֲ�ֱ��ͼ
��3��Ϊ�˼���ѧ����ǿ��ȫ��ʶ�����������ӳ���90�ֵ�ѧ����ѡ2�˽���ѧϰ���飬��ôȡ��100�ֵ�С����С��ͬʱ��ѡ�ϵĸ����Ƕ��٣������б�������״ͼ����˵�������г����еȿ��ܽ����
Ƶ���ֲ���
���飨�֣� | Ƶ�� | Ƶ�� |
50��x 60 | 2 | 0.04 |
60��x 70 | 12 | a |
70��x��80 | b | 0.36 |
80��x 90 | 14 | 0.28 |
90��x 100 | c | 0.08 |
�ϼ� | 50 | 1 |