题目内容
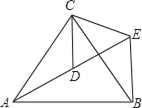
【题目】已知:点O是平行四边形ABCD两条对角线的交点,点P是AC所在直线上的一个动点(点P不与点A、C重合),分别过点A、C向直线BP作垂线,垂足分别为E、F
(1)如图1,当点P与点O重合时,求证:OE=OF
(2)直线BP绕点B逆时针方向旋转,当∠OFE=![]() 时,有OE=OF,如图2,线段CF、AE、OE之间有怎样的数量关系?给出证明。
时,有OE=OF,如图2,线段CF、AE、OE之间有怎样的数量关系?给出证明。
(3)当点P在图3位置,且∠OFE=![]() 时,线段CF、AE、OE之间有怎样的数量关系?(直接写出结论,无需证明.
时,线段CF、AE、OE之间有怎样的数量关系?(直接写出结论,无需证明.

【答案】(1)(2)证明见解析;(3)CF=OE-AE.
【解析】
(1)由△AOE≌△COF即可得出结论.
(2)图2中的结论为:CF=OE+AE,延长EO交CF于点G,只要证明△EOA≌△GOC,△OFG是等边三角形,即可解决问题.
(3)图3中的结论为:CF=OE-AE,延长EO交FC的延长线于点G,证明方法类似.
(1)∵![]() 重合
重合
∴![]()
∵四边形ABCD是平行四边形,O为对角线交点
∴AO=CO,
在△AEO和△CFO中,

∴△AEO![]() △CFO(AAS)
△CFO(AAS)
∴OE=OF
(2)延长EO交CF于点G,如图所示,

则可得![]()
∵![]()
∴AE∥CF
∴![]()
又∵O 为对角线交点
∴AO=CO
在△AEO和△CGO中,
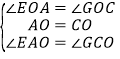
∴△AEO![]() △CGO(ASA)
△CGO(ASA)
∴OE=OG,AE=CG
在Rt△EFG中,OE=OG,
∴点O为Rt△EFG斜边EG的中点,
故OF=OE=OG=![]()
∴∠OFE=∠OEF=30°
∴∠OFG=∠EFG![]() ∠OFE=90°
∠OFE=90°![]() 30°=60°
30°=60°
又∵OF=OG
∴△OFG为等边三角形
故GF=OF=OE
∵CF=CG+GF
∴CF=CG+GF =AE+OE
(3)延长EO、FC交于点G,如图所示,

∵![]()
∴AE∥CF
∴![]()
又∵O 为对角线交点
∴AO=CO
在△AEO和△CGO中,
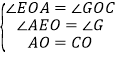
∴△AEO![]() △CGO(AAS)
△CGO(AAS)
∴OE=OG,AE=CG
在Rt△EFG中,OE=OG,
故点O为Rt三角形EFG斜边EG的中点,
∴OF=OE=OG=![]()
∵∠OEF=30°
∴∠OFE=∠OEF=30°
即∠OFG=∠EFG-∠EFO=90°![]() 30°=60°
30°=60°
又∵OF=OG
∴△OFG为等边三角形
∴GF=OF=OG=OE
∵CF=GF-CG
∴CF=OE-AE

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案【题目】某宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与其价格x(元)(180≤x≤300)满足一次函数关系,部分对应值如表:
x(元) | 180 | 260 | 280 | 300 |
y(间) | 100 | 60 | 50 | 40 |
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每日空置的客房需支出各种费用60元,当房价为多少元时,宾馆当日利润最大?求出最大值.(宾馆当日利润=当日房费收入﹣当日支出)
【题目】2016年黔西南州教育局组织全州中小学生参加全省安全知识网络竞赛,在全州安全知识竞赛结束后,通过网上查询,某校一名班主任对本班成绩(成绩取整数,满分100分)作了统计分析,绘制成如下频数分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题: 
(1)频数分布表中a= , b= , c=
(2)补全频数分布直方图
(3)为了激励学生增强安全意识,班主任准备从超过90分的学生中选2人介绍学习经验,那么取得100分的小亮和小华同时被选上的概率是多少?请用列表法或画树状图加以说明,并列出所有等可能结果.
频数分布表
分组(分) | 频数 | 频率 |
50<x 60 | 2 | 0.04 |
60<x 70 | 12 | a |
70<x<80 | b | 0.36 |
80<x 90 | 14 | 0.28 |
90<x 100 | c | 0.08 |
合计 | 50 | 1 |