题目内容
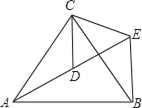
【题目】如图，AC⊥BC，AC=BC，D是BC上一点，连接AD，与∠ACB的平分线交于点E，连接BE．若S△ACE= 
，S△BDE= 
，则AC= ． 
【答案】2
【解析】解：过E作AC，BC的垂线，垂足分别为F，G，
设BC=4x，则AC=4x，
∵CE是∠ACB的平分线，EF⊥AC，EG⊥BC，
∴EF=EG，又S△ACE= 
，S△BDE= 
，
∴BD= 
AC=x，
∴CD=3x，
∵四边形EFCG是正方形，
∴EF=FC，
∵EF∥CD，
∴ 
= 
，即 
= 
，
解得，EF= 
x，
则 
×4x× x= ，
解得，x= ，
则AC=4x=2，
所以答案是：2．
【考点精析】通过灵活运用角平分线的性质定理和相似三角形的判定与性质，掌握定理1：在角的平分线上的点到这个角的两边的距离相等； 定理2：一个角的两边的距离相等的点，在这个角的平分线上；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方即可以解答此题．
【题目】某宾馆拥有客房100间，经营中发现：每天入住的客房数y（间）与其价格x（元）（180≤x≤300）满足一次函数关系，部分对应值如表：
x（元） | 180 | 260 | 280 | 300 |
y（间） | 100 | 60 | 50 | 40 |
（1）求y与x之间的函数表达式；
（2）已知每间入住的客房，宾馆每日需支出各种费用100元；每日空置的客房需支出各种费用60元，当房价为多少元时，宾馆当日利润最大？求出最大值．（宾馆当日利润=当日房费收入﹣当日支出）
【题目】上网流量、语音通话是手机通信消费的两大主体，目前，某通信公司推出消费优惠新招﹣﹣“定制套餐”，消费者可根据实际情况自由定制每月上网流量与语音通话时间，并按照二者的阶梯资费标准缴纳通信费．下表是流量与语音的阶梯定价标准．
流量阶梯定价标准 | |
使用范围 | 阶梯单价（元/MB） |
1﹣100MB | a |
101﹣500MB | 0.07 |
501﹣20GB | b |
语音阶梯定价标准 | |
使用范围 | 阶梯资费（元/分钟） |
1﹣500分钟 | 0.15 |
501﹣1000分钟 | 0.12 |
1001﹣2000分钟 | m |
【小提示：阶梯定价收费计算方法，如600分钟语音通话费=0.15×500+0.12×（600﹣500）=87元】
（1）甲定制了600MB的月流量，花费48元；乙定制了2GB的月流量，花费120.4元，求a，b的值．（注：1GB=1024MB）
（2）甲的套餐费用为199元，其中含600MB的月流量；丙的套餐费用为244.2元，其中包含1GB的月流量，二人均定制了超过1000分钟的每月通话时间，并且丙的语音通话时间比甲多300分钟，求m的值．
