Question

【题目】某企业接到一批帽子生产任务，按要求在20天内完成，约定这批帽子的出厂价为每顶8元．为按时完成任务，该企业招收了新工人，设新工人小华第x天生产的帽子数量为y顶，y与x满足如下关系式：y＝

（1）小华第几天生产的帽子数量为220顶？

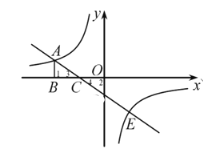
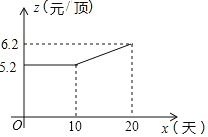
（2）如图，设第x天每顶帽子的成本是P元，P与x之间的关系可用图中的函数图象来刻画．若小华第x天创造的利润为w元，求w与x之间的函数表达式，并求出第几天的利润最大？最大值是多少元？

（3）设（2）小题中第m天利润达到最大值，若要使第（m+1）天的利润比第m天的利润至少多49元，则第（m+1）天每顶帽子至少应提价几元？

Answer 1

【答案】（1）小华第12天生产的帽子数量为220顶；（2）当x＝14时，w有最大值，最大值为576元；（3）第15天每顶帽子至少应提价0.2元．

【解析】

（1）把代入，解方程即可求得；

（2）根据图象求得成本p与x之间的关系，然后根据利润等于订购价减去成本价，然后整理即可得到W与x的关系式，再根据一次函数的增减性和二次函数的增减性解答；

（3）根据（2）得出，根据利润等于订购价减去成本价得出提价a与利润w的关系式，再根据题意列出不等式求解即可

解：（1）若，则，与不符，

∴，

解得:，

故第12天生产了220顶帽子；

（2）由图象得，

当时，；

当时，设，

把代入上式，得

，

解得， ，

∴

①时，

当时，w有最大值为（元）

②时，，当时，w有最大值，最大值为560（元）；

③时，

当时，w有最大值，最大值为576（元）．

综上，当时，w有最大值，最大值为576元．

（3）由（2）小题可知，，设第15天提价a元，由题意得

∴

∴

答：第15天每顶帽子至少应提价0.2元．