题目内容
【题目】如图，点
是反比例函数
图象上一点，
轴于点
，
是
的中点．一次函数
经过，两点，
．
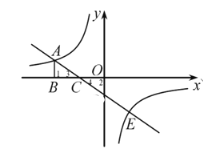
（1）求反比例函数和一次函数的解析式．
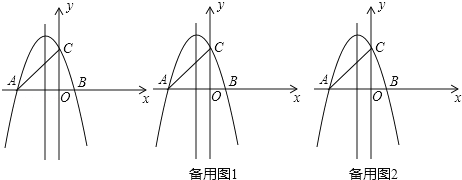
（2）画出反比例函数的另一支图象，写出自变量
取何值时，使反比例函数的函数值大于一次函数的函数值．
【答案】（1）
，
；（2）图见解析，
，或
【解析】
（1）如图，首先求出一次函数
与
轴的交点
，再通过证明
及由
，求出A点的坐标，将A点坐标分别代入一次函数及反比例函数中即可求出反比例函数和一次函数的解析式；
（2）首先求出E点坐标，再观察图象知，反比例函数的图象在一次函数的上面的部分对应的x的值即为取值范围．
解：（1）如图，一次函数与轴的交点．
∴
．
∵
轴，∴
．
∵
，
，
∴．
∴
．
∵，∴
．∴
．
∴
．∴
．
将代入
，得
．
代入，得
．∴
．
∴反比例函数解析式为，
一次函数解析式．
（2）如图，考查点
的坐标，由
，
整理，得
．解得
，或
．
∴
．
由图象知，当，或时，
反比例函数的函数值大于一次函数的函数值．
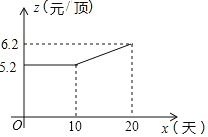
备战中考寒假系列答案
【题目】如图，半圆O的直径AB＝5cm，点C是半圆O上的动点，连结AC、BC．设AC＝x（单位：cm），△ABC的面积为y（单位：cm2，当点C与A、B重合时，y的值为0）．轩轩根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．
下面是轩轩的探究过程，请补充完整：
（1）按照下表中自变量x的值进行取点、画图、测量，分别得到了x与y的几组值，结果如表：
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 |
y/cm2 | 0 | 1.25 | 2.45 | 3.58 | 4.57 | 5.41 | 6.25 | 4.91 | 0 |
该函数的表达式为__________，自变量x的取值范围为___________．
（2）在右图中建立平面直角坐标系，描出以补全后的表中各组对应值为坐标的点，画出该函数的图象．
（3）结合画出的函数图象，解决问题：在（2）问的直角坐标系中画出直线y1＝x，根据图象得出当y＝y1时x的正数值约为_______（精确到0.1）
