Question

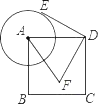
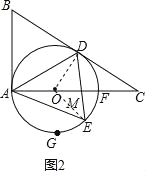
【题目】如图，在Rt△ABC中，∠BAC=90°，∠C=30°，以边上AC上一点O为圆心，OA为半径作⊙O，⊙O恰好经过边BC的中点D，并与边AC相交于另一点F．

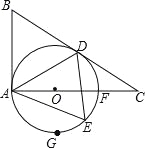
（1）求证：BD是⊙O的切线．

（2）若AB=，E是半圆上一动点，连接AE，AD，DE．

填空：

①当的长度是____________时，四边形ABDE是菱形；

②当的长度是____________时，△ADE是直角三角形．

Answer 1

【答案】（1）见解析；（2）①；②π或π．

【解析】

试题分析：（1）证明：如图1，连接OD，∵在Rt△ABC中，∠BAC=90°，∠C=30°，∴AB=BC，∵D是BC的中点，∴BD=BC，∴AB=BD，∴∠BAD=∠BDA，∵OA=OD，∴∠OAD=∠ODA，∴∠ODB=∠BAO=90°，即OD⊥BC，∴BD是⊙O的切线．

（2）①当DE⊥AC时，四边形ABDE是菱形；如图2，设DE交AC于点M，连接OE，则DE=2DM，∵∠C=30°，∴CD=2DM，∴DE=CD=AB=BC，∵∠BAC=90°，∴DE∥AB，∴四边形ABDE是平行四边形，∵AB=BD，∴四边形ABDE是菱形；∵AD=BD=AB=CD=BC=，∴△ABD是等边三角形，OD=CDtan30°=1，∴∠ADB=60°，∵∠CDE=90°﹣∠C=60°，∴∠ADE=180°﹣∠ADB﹣∠CDE=60°，∴∠AOE=2∠ADE=120°，∴的长度为： =π；故答案为：；

②若∠ADE=90°，则点E与点F重合，此时的长度为： =π；若∠DAE=90°，则DE是直径，则∠AOE=2∠ADO=60°，此时的长度为： =π；∵AD不是直径，∴∠AED≠90°；综上可得：当的长度是π或π时，△ADE是直角三角形．故答案为：π或π．