题目内容
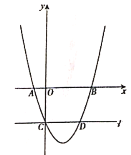
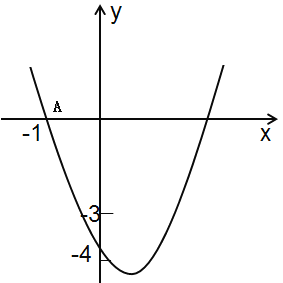
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,顶点坐标为
,顶点坐标为![]() ,与
,与![]() 轴的交点在
轴的交点在![]() ,
,![]() 之间(包含端点),以下结论: ①
之间(包含端点),以下结论: ①![]() ;②
;②![]() ;③
;③![]() ;④关于
;④关于![]() 的方程
的方程![]() 没有实数根.其中正确的结论有( )
没有实数根.其中正确的结论有( )
A.4个B.3个C.2个D.1个
【答案】A
【解析】
利用抛物线开口方向得到a>0,再由抛物线的顶点![]() ,得对称轴为
,得对称轴为![]() ,则抛物线与x轴的另一个交点为(3,0),当x=2,则y<0,于是可对①进行判断;利用
,则抛物线与x轴的另一个交点为(3,0),当x=2,则y<0,于是可对①进行判断;利用![]() ≤c≤
≤c≤![]() 和c=-3a可对②进行判断;由b=-2a,c=-3a,a+b+c=m,求出a、c的值,可对③进行判断;根据抛物线y=ax2+bx+c与直线y=m-1没有交点可对④进行判断.
和c=-3a可对②进行判断;由b=-2a,c=-3a,a+b+c=m,求出a、c的值,可对③进行判断;根据抛物线y=ax2+bx+c与直线y=m-1没有交点可对④进行判断.
解:由题意可知,![]() ,
,
∵抛物线的顶点为![]() ,
,
∴对称轴为![]() ,
,
∴![]() ,
,
∵抛物线与![]() 轴交于点
轴交于点![]() ,
,
∴抛物线与x轴的另一个交点坐标为(3,0),
当x=2,则y<0,
∴![]() ,
,
∴![]() ;故①正确;
;故①正确;
∵抛物线经过点![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵抛物线与![]() 轴的交点在
轴的交点在![]() ,
,![]() 之间(包含端点),
之间(包含端点),
∴![]() ,
,
∴![]() ,
,
∴![]() ;故②正确;
;故②正确;
当![]() 时,有
时,有![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;故③正确;
;故③正确;
∵抛物线的顶点为![]() ,且
,且![]() ,
,
∴抛物线y=ax2+bx+c与直线y=m-1没有交点,
∴关于![]() 的方程
的方程![]() 没有实数根;故④正确;
没有实数根;故④正确;
故选:A.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
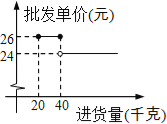
小学生10分钟应用题系列答案【题目】王妈妈在莲花商场里购买单价总和是90元的商品甲、乙、丙共两次,其中甲的单价是20元,乙的单价是40元,甲商品第一次购买的数量是第二次购买数量的两倍,乙商品第一次购买的数量与丙商品第二次购买的数量相等,两次购买商品甲、乙、丙的数量和总费用如下表:
购买商品甲的 数量(个) | 购买商品乙的 数量(个) | 购买商品丙的 数量(个) | 购买总费用(元) | |
第一次购物 | 4 | 440 | ||
第二次购物 | 7 | 490 |
(1)求两次购买甲、乙、丙三种商品的总数量分别是多少?
(2)由于莲花商场物美价廉,王妈妈打算第三次前往购买商品甲、乙、丙,设三种商品的数量总和为a个,其中购买乙商品数量是甲商品数量的3倍,购买总费用为1 280元,求a的最小值.