题目内容
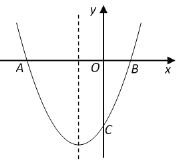
【题目】如图，在平面直角坐标系中，已知抛物线
与
轴交于
，
两点(点在点的左侧)，与
轴交于点
，经过点的直线
与该抛物线交于另一点
，并且直线
轴，点
为该抛物线上一个动点，点
为直线上一个动点．
（1）当
，且
时，连接
，
，求证：四边形
是平行四边形
（2）当
时，连接，线段与线段
交于点
，
，且
，连接
，求线段的长；
（3）连接
，
，试探究：是否存在点
，使得
与
互为余角?若存在，求出点的坐标；若不存在，请说明理由．
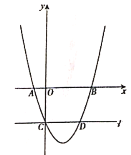
【答案】（1）见解析；（2）
；（3）存在，
【解析】
（1）由二次函数的性质，先求出点A、B、C的坐标，然后得到点D的坐标，则得到
与
的值，把点P代入抛物线，求出m的值，由平行四边形的判定，即可得到答案；
（2）由题意，表示PQ的长度，然后求出
，
，再由
，得到
，即可得到答案；
（3）根据题意，利用三角函数得到
，然后分两种情况进行分类讨论：①当点
在直线
上方时，
；②当点在直线下方时，
，
；分别求出m的值，即可得到点P的坐标．
解：如图：
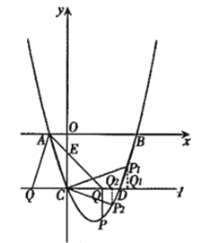
（1）证明：当
时，
，
解得
，
，
.
当
时，
，
.
∵直线
轴，
∴直线的解析式为.
，
解得
，
，
.
∵点
在直线上，
.
，
，点
在该抛物线上，
解得
或
(舍去).
∵直线轴，
，
，
，
∴四边形
是平行四边形.
（2）
两点的横坐标都是
，
∴直线轴，
设
，则
，
，
解得：
或
.
，
，.
∵直线轴，
，
∴，
，
，
,
，
；
（3）假设存在点，使得
与
互为余角，即
.
，
.
，
连接
.
∵直线轴，直线
轴，
是直角三角形，且
.
①当点在直线上方时，
(i)若点在
轴左侧，则
，
.
，解得
(舍去)，
(舍去).
(ii)若点在轴右侧，则，
.
，解得
(舍去)，
.
，
②当点在直线下方时，，
，解得
(舍去)，
，
；
综上，存在点，使得与互为余角．
【题目】为培养学生良好学习习惯，某学校计划举行一次“整理错题集”的展示活动，对该校部分学生“整理错题集”的情况进行了一次抽样调查，根据收集的数据绘制了下面不完整的统计图表．
整理情况 | 频数 | 频率 |
非常好 | 0.21 | |
较好 | 70 | 0.35 |
一般 | m | |
不好 | 36 |
请根据图表中提供的信息，解答下列问题：
（1）本次抽样共调查了 名学生；
（2）m= ；
（3）该校有1500名学生，估计该校学生整理错题集情况“非常好”和“较好”的学生一共约多少名？
（4）某学习小组4名学生的错题集中，有2本“非常好”（记为A1、A2），1本“较好”（记为B），1本“一般”（记为C），这些错题集封面无姓名，而且形状、大小、颜色等外表特征完全相同，从中抽取一本，不放回，从余下的3本错题集中再抽取一本，请用“列表法”或“画树形图”的方法求出两次抽到的错题集都是“非常好”的概率．
