��Ŀ����
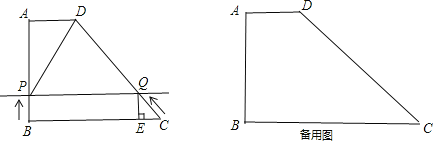
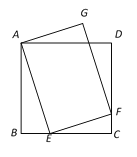
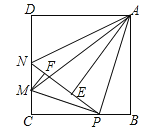
����Ŀ����ͼ���ڱ߳�Ϊ4��������ABCD�У�P��BC����һ���㣨����B��C���㣩������ABP��ֱ��AP���ۣ���B���ڵ�E������CD����һ��M��ʹ�ý���CMP��ֱ��MP���ۺ�C����ֱ��PE�ϵĵ�F����ֱ��PE��CD�ڵ�N������MA��NA�������½�������ȷ���У� ��
�١�CMP�ס�BPA��
���ı���AMCB��������ֵΪ10��
����PΪBC�е�ʱ��AEΪ�߶�NP���д��ߣ�
���߶�AM����СֵΪ2![]() ��
��
�ݵ���ABP�ա�ADNʱ��BP= 4![]() -4��
-4��
A. 1��B. 2��C. 4��D. 3��
���𰸡�D
��������
�������������ε��ж������������������. ֤AB=CB=DC=AD=4����C=��B=90�����á�CMP�ס�BPA���ʢ���ȷ����x=2ʱ���ı���AMCB������ֵΪ10���ʢ���ȷ��NE��EP���ʢ۴���AM����Сֵ=![]() =5���ʢܴ���PB=
=5���ʢܴ���PB=![]() �ʢ���ȷ��
�ʢ���ȷ��
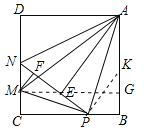
�ߡ�APB=��APE����MPC=��MPN���ߡ�CPN+��NPB=180������2��NPM+2��APE=180�������MPN+��APE=90�������APM=90�����ߡ�CPM+��APB=90������APB+��PAB=90�������CPM=��PAB�����ı���ABCD�������Σ���AB=CB=DC=AD=4����C=��B=90�������CMP�ס�BPA���ʢ���ȷ����PB=x����CP=4��x���ߡ�CMP�ס�BPA����![]() ����CM=
����CM=![]() x��4��x������S�ı���AMCB=
x��4��x������S�ı���AMCB=![]() [4+
[4+![]() x��4��x��]��4=
x��4��x��]��4=![]() =
=![]() ����x=2ʱ���ı���AMCB������ֵΪ10���ʢ���ȷ����PB=PC=PE=2ʱ����ND=NE=y����Rt��PCN�У�
����x=2ʱ���ı���AMCB������ֵΪ10���ʢ���ȷ����PB=PC=PE=2ʱ����ND=NE=y����Rt��PCN�У�![]() ���
���![]() ����NE��EP���ʢ۴�����MG��AB��G����AM=
����NE��EP���ʢ۴�����MG��AB��G����AM=![]() =
=![]() ����AG��СʱAM��С����AG=AB��BG=AB��CM=4��
����AG��СʱAM��С����AG=AB��BG=AB��CM=4��![]() x��4��x��=
x��4��x��=![]() ����x=1ʱ��AG��Сֵ=3����AM����Сֵ=
����x=1ʱ��AG��Сֵ=3����AM����Сֵ=![]() =5���ʢܴ��ߡ�ABP�ա�ADNʱ�����PAB=��DAN=22.5������AB��ȡһ��Kʹ��AK=PK����PB=z�����KPA=��KAP=22.5�����ߡ�PKB=��KPA+��KAP=45�������BPK=��BKP=45������PB=BK=z��AK=PK=
=5���ʢܴ��ߡ�ABP�ա�ADNʱ�����PAB=��DAN=22.5������AB��ȡһ��Kʹ��AK=PK����PB=z�����KPA=��KAP=22.5�����ߡ�PKB=��KPA+��KAP=45�������BPK=��BKP=45������PB=BK=z��AK=PK=![]() z����z+
z����z+![]() z=4����z=
z=4����z=![]() ����PB=
����PB=![]() �ʢ���ȷ��
�ʢ���ȷ��
��ѡ��C��

����Ŀ��ij��˾������һ����Ʒ�������ۣ��ò�Ʒ�Ľ�������Ϊ6Ԫ/���������г����飬�ò�Ʒ����������y�����������۵���x��Ԫ/����֮������һ�κ�����ϵ��������������y�����������۵���x��Ԫ/�����ļ������������
x | 10 | 12 | 14 | 16 |
y | 300 | 240 | 180 | m |
��1�����y��x֮��ĺ�����ϵʽ����Ҫ��д���Ա�����ȡֵ��Χ����m��ֵ��
��2�����գ�1���е����۹��ɣ������۵��۶�Ϊ17.5Ԫ/��ʱ����������Ϊ�� ��������ʱ������������������� ����
��3��Ϊ�������գ��ù�˾���ս����ɱ�������900����900Ԫ�����ڣ����գ�1���е����۹��ɣ�Ҫʹ������������������۵���Ӧ��Ϊ���٣��������ʱ���������