ЬтФПФкШн
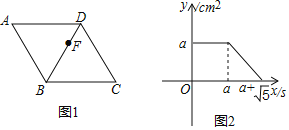
ЁОЬтФПЁПШчЭМЃЌвбжЊЬнаЮABCDжаЃЌADЁЮBCЃЌADЃН2ЃЌABЃНBCЃН8ЃЌCDЃН10ЃЎ
(1)ЧѓЬнаЮABCDЕФУцЛ§SЃЛ
(2)ЖЏЕуPДгЕуBГіЗЂЃЌвд1cm/sЕФЫйЖШЃЌбиBADCЗНЯђЃЌЯђЕуCдЫЖЏЃЛЖЏЕуQДгЕуCГіЗЂЃЌвд1cm/sЕФЫйЖШЃЌбиCDAЗНЯђЃЌЯђЕуAдЫЖЏЃЌЙ§ЕуQзїQEЁЭBCгкЕуEЃЎШєPЁЂQСНЕуЭЌЪБГіЗЂЃЌЕБЦфжавЛЕуЕНДяФПЕФЕиЪБећИідЫЖЏЫцжЎНсЪјЃЌЩшдЫЖЏЪБМфЮЊtУыЃЎЮЪЃК
ЂйЕБЕуPдкBAЩЯдЫЖЏЪБЃЌЪЧЗёДцдкетбљЕФtЃЌЪЙЕУжБЯпPQНЋЬнаЮABCDЕФжмГЄЦНЗжЃПШєДцдкЃЌЧыЧѓГіtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЂкдкдЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдкетбљЕФtЃЌЪЙЕУвдPЁЂAЁЂDЮЊЖЅЕуЕФШ§НЧаЮгыЁїCQEЯрЫЦЃПШєДцдкЃЌЧыЧѓГіЫљгаЗћКЯЬѕМўЕФtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЂлдкдЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдкетбљЕФtЃЌЪЙЕУвдPЁЂDЁЂQЮЊЖЅЕуЕФШ§НЧаЮЧЁКУЪЧвдDQЮЊвЛбќЕФЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГіЫљгаЗћКЯЬѕМўЕФtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
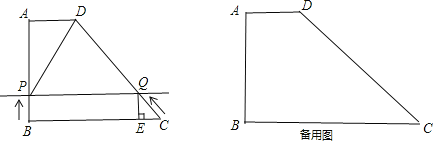
ЁОД№АИЁП(1)SABCDЃН40ЃЛ(2)ЂйЕБtЃН3УыЪБЃЌPQНЋЬнаЮABCDжмГЄЦНЗжЃЛЂкtЃН![]() ЛђtЃН
ЛђtЃН![]() ЪБЃЌЁїPADгыЁїCQEЯрЫЦЃЛЂлtЃН
ЪБЃЌЁїPADгыЁїCQEЯрЫЦЃЛЂлtЃН![]() Лђ8ЁмtЃМ10Лђ10ЃМtЁм12ЪБЃЌвдDQЮЊбќЕФЕШбќЁїDPQГЩСЂЃЎ
Лђ8ЁмtЃМ10Лђ10ЃМtЁм12ЪБЃЌвдDQЮЊбќЕФЕШбќЁїDPQГЩСЂЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЧѓУцЛ§вЊЯШЧѓЬнаЮЕФИпЃЌПЩИљОнСНЕзЕФВюКЭCDЕФГЄЃЌдкжБНЧШ§НЧаЮжагУЙДЙЩЖЈРэНјааЧѓНтЃЌЕУГіИпКѓМДПЩЧѓГіЬнаЮЕФУцЛ§ЃЎ
ЃЈ2ЃЉЂйPQЦНЗжЬнаЮЕФжмГЄЃЌФЧУДAD+DQ+AP=BC+CQ+BPЃЌвбжЊСЫADЃЌBCЕФГЄЃЌПЩвдгУtРДБэЪОГіAPЃЌBPЃЌCQЃЌQDЕФГЄЃЌФЧУДПЩИљОнЩЯУцЕФЕШСПЙиЯЕЧѓГіtЕФжЕЃЎ
ЂкБОЬтвЊЗжШ§жжЧщПіНјааЬжТлЃК
вЛЃЌЕБPдкABЩЯЪБЃЌМД0ЃМtЁм8ЃЌШчЙћСНШ§НЧаЮЯрЫЦЃЌФЧУДЁЯC=ЁЯADPЃЌЛђЁЯC=ЁЯAPDЃЌФЧУДдкЁїADPжаИљОнЁЯCЕФе§ЧажЕЃЌЧѓГіtЕФжЕЃЎ
ЖўЃЌЕБPдкADЩЯЪБЃЌМД8ЃМtЁм10ЃЌгЩгкPЃЌAЃЌDдквЛЬѕжБЯпЩЯЃЌвђДЫЙЙВЛГЩШ§НЧаЮЃЎ
Ш§ЃЌЕБPдкCDЩЯЪБЃЌМД10ЃМtЁм12ЃЌгЩгкЁЯADCЪЧИіЖлНЧЃЌвђДЫЁїADPЪЧИіЖлНЧШ§НЧаЮвђДЫВЛПЩФмКЭжБНЧЁїCQEЯрЫЦЃЎ
злКЯШ§жжЧщПіМДПЩЕУГіЗћКЯЬѕМўЕФtЕФжЕЃЎ
ЃЈ3ЃЉКЭЃЈ2ЃЉЯрЭЌвВвЊЗжШ§жжЧщПіНјааЬжТлЃК
вЛЃЌЕБPдкABЩЯЪБЃЌМД0ЃМtЁм8ЃЌЕШбќЁїPDQвдDQЮЊбќЃЌвђДЫDQ=DPЛђDQ=PQЃЌПЩвдЭЈЙ§ЙЙНЈжБНЧШ§НЧаЮРДБэЪОГіDPЃЌPQЕФГЄЃЌШЛКѓИљОнЕУГіЕФЕШСПЙиЯЕРДЧѓtЕФжЕЃЎ
ЖўЃЌЕБPдкADЩЯЪБЃЌМД8ЃМtЁм10ЃЌгЩгкBA+AD=CD=10ЃЌвђДЫDP=DQ=10-tЃЌвђДЫDPЃЌDQКуЯрЕШЃЎ
Ш§ЃЌЕБPдкCDЩЯЪБЃЌМД10ЃМtЁм12ЃЌЧщПіЭЌЖўЃЎ
злКЯШ§жжЧщПіПЩЕУГіЕШбќШ§НЧаЮвдDQЮЊбќЪБЃЌtЕФШЁжЕЃЎ
(1)Й§DзїDHЁЮABНЛBCгкHЕуЃЌ
ЁпADЁЮBHЃЌDHЁЮABЃЌ
ЁрЫФБпаЮABHDЪЧЦНааЫФБпаЮЃЎ
ЁрDHЃНABЃН8ЃЛBHЃНADЃН2ЃЎ
ЁрCHЃН8Љ2ЃН6ЃЎ
ЁпCDЃН10ЃЌ
ЁрDH2+CH2ЃНCD2ЁрЁЯDHCЃН90ЁуЃЎ
ЁЯBЃНЁЯDHCЃН90ЁуЃЎ
ЁрЬнаЮABCDЪЧжБНЧЬнаЮЃЎ
ЁрSABCDЃН![]()
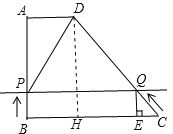
(2)ЂйЁпBPЃНCQЃНtЃЌ
ЁрAPЃН8ЉtЃЌDQЃН10ЉtЃЌ
ЁпAP+AD+DQЃНPB+BC+CQЃЌ
Ёр8Љt+2+10ЉtЃНt+8+tЃЎ
ЁрtЃН3ЃМ8ЃЎ
ЁрЕБtЃН3УыЪБЃЌPQНЋЬнаЮABCDжмГЄЦНЗжЃЎ
ЂкЕквЛжжЧщПіЃК0ЃМtЁм8ШєЁїPADЁзЁїQECдђЁЯADPЃНЁЯC
ЁрtanЁЯADPЃНtanЁЯCЃН![]()
Ёр![]()
ЁрtЃН![]()
ШєЁїPADЁзЁїCEQдђЁЯAPDЃНЁЯC
ЁрtanЁЯAPDЃНtanЁЯCЃН![]()
Ёр![]()
ЁрtЃН![]()
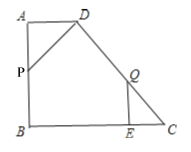
ЕкЖўжжЧщПіЃК8ЃМtЁм10ЃЌPЁЂAЁЂDШ§ЕуВЛФмзщГЩШ§НЧаЮЃЛ
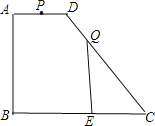
ЕкШ§жжЧщПіЃК10ЃМtЁм12ЃЌЁїADPЮЊЖлНЧШ§НЧаЮгыRtЁїCQEВЛЯрЫЦЃЛ
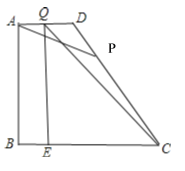
ЁрtЃН![]() ЛђtЃН
ЛђtЃН![]() ЪБЃЌЁїPADгыЁїCQEЯрЫЦЃЎ
ЪБЃЌЁїPADгыЁїCQEЯрЫЦЃЎ
ЂлЕквЛжжЧщПіЃКЕБ0ЁмtЁм8ЪБЃЎЙ§QЕузїQEЁЭBCЃЌQHЁЭABЃЌДЙзуЮЊEЁЂHЃЎ
ЁпAPЃН8ЉtЃЌADЃН2ЃЌ
ЁрPDЃН![]()
ЁпCEЃН![]() tЃЌQEЃН
tЃЌQEЃН![]() tЃЌ
tЃЌ
ЁрQHЃНBEЃН8Љ![]() tЃЌBHЃНQEЃН
tЃЌBHЃНQEЃН![]() tЃЎ
tЃЎ
ЁрPHЃНtЉ![]() tЃН
tЃН![]() tЃЎ
tЃЎ
ЁрPQЃН![]() ЃЌDQЃН10ЉtЃЎ
ЃЌDQЃН10ЉtЃЎ
ЂёЃКDQЃНDPЃЌ10ЉtЃН![]() ЃЌ
ЃЌ
НтЕУtЃН8УыЃЎ
ЂђЃКDQЃНPQЃЌ10ЉtЃН![]()
ЛЏМђЕУЃК3t2Љ52t+180ЃН0
НтЕУЃКtЃН![]() ЃЌtЃН
ЃЌtЃН![]() ЃО8(ВЛКЯЬтвтЩсШЅ)
ЃО8(ВЛКЯЬтвтЩсШЅ)
ЁрtЃН![]()
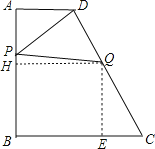
ЕкЖўжжЧщПіЃК8ЁмtЁм10ЪБЃЎDPЃНDQЃН10ЉtЃЎ
ЁрЕБ8ЁмtЃМ10ЪБЃЌвдDQЮЊбќЕФЕШбќЁїDPQКуГЩСЂЃЎ
ЕкШ§жжЧщПіЃК10ЃМtЁм12ЪБЃЎDPЃНDQЃНtЉ10ЃЎ
ЁрЕБ10ЃМtЁм12ЪБЃЌвдDQЮЊбќЕФЕШбќЁїDPQКуГЩСЂЃЎ
злЩЯЫљЪіЃЌtЃН![]() Лђ8ЁмtЃМ10Лђ10ЃМtЁм12ЪБЃЌвдDQЮЊбќЕФЕШбќЁїDPQГЩСЂЃЎ
Лђ8ЁмtЃМ10Лђ10ЃМtЁм12ЪБЃЌвдDQЮЊбќЕФЕШбќЁїDPQГЩСЂЃЎ

 аТПЮБъПьРжЬсгХЪюМйзївЕЩТЮїТУгЮГіАцЩчЯЕСаД№АИ
аТПЮБъПьРжЬсгХЪюМйзївЕЩТЮїТУгЮГіАцЩчЯЕСаД№АИ