题目内容
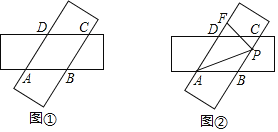
【题目】如图，点D是线段AB上的任意一点（不与点A和B重合），C是线段AD的中点，AB=4cm.
（1）若D是线段AB的中点，求线段CD的长度.
（2）在图中作线段DB的中点E，当点D在线段AB上从左向右移动时，试探究线段CE长度的变化情况.
【答案】（1）1cm；（2）线段CE=2cm，长度不会变化，理由见解析．
【解析】
（1）根据线段中点定义计算即可；
（2）作出图形，根据线段中点定义计算即可．
（1）∵D是线段AB的中点，
∴AD=DB=
AB=2(cm)．
∵C是线段AD的中点，
∴CD=AD=1(cm)．
（2）如图，线段CE的长不会变化．理由如下：
∵C是线段AD的中点，
∴CD=AD．
∵E是线段DB的中点，
∴DE=DB，
∴CE=CD+DE=AD+DB=(AD+DB)=AB=2(cm)．
练习册系列答案
相关题目
【题目】某商场计划购进甲、乙两种运动鞋，其中甲、乙两种运动鞋的进价和售价如表（进价大于50元）
运动鞋价格 | 甲 | 乙 |
进价（元/双） | m | m﹣4 |
售价（元/双） | 160 | 150 |
已知：用3000元购进甲种运动鞋的数量比用2400元购进乙种运动鞋的数量多5．
（1）求m的值；
（2）设该商场应购进甲种运动鞋t双，两种鞋共200双，商场销售完这批鞋可获利y元，请求出y关于t的函数解析式；
（3）商场计划在（2）的条件下，总进价不低于19520元，且不超过19532元，问该专卖店有哪几种进货方案？
（4）求该专卖店要获得最大利润的进货方案及最大利润．
