题目内容
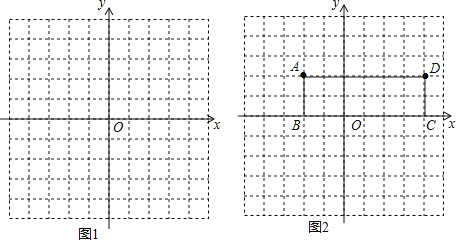
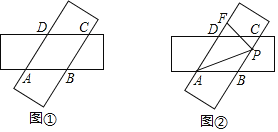
【题目】两张宽度均为4的矩形纸片按如图所示方式放置:
(1)如图1,求证:四边形ABCD是菱形;
(2)如图2,点P在BC上,PF![]() AD于点F,若
AD于点F,若![]() =16
=16![]() , PC=1.
, PC=1.
①求∠BAD的度数;②求DF的长.
【答案】(1)见解析;(2)45°;DF=3.
【解析】
(1)过点D作DE⊥AB于E,作DQ⊥BC于Q,构造全等三角形,得出AD=CD,再根据AB∥CD,AD∥BC,得到四边形ABCD是平行四边形,进而得出四边形ABCD是菱形;
(2)①先根据菱形的面积求得菱形的边长,再根据sin∠DAE的值,求得∠BAD的度数;②根据CP=1,以及∠PCG=∠BAD=45°,求得PG=1,再根据∠CDF=45°=∠DGF,即可得到DF=FG=1.
(1)如图1,过点D作DE⊥AB于E,作DQ⊥BC于Q,则∠AED=∠CQD=90°,
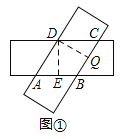
∵矩形纸片宽度均为4,
∴DE=DQ,
又∵∠CDE=∠ADQ=90°,
∴∠ADE=∠CDQ,
在△ADE和△CDQ中,
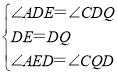 ,
,
∴△ADE≌△CDQ(ASA),
∴AD=CD,
又∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∴四边形ABCD是菱形;
(2)①如图1,∵S四边形ABCD=16![]() ,
,
∴AB×DE=16![]() ,即AB×4=16
,即AB×4=16![]() ,
,
∴AB=4![]() =AD,
=AD,
∴sin∠DAE=![]() ,
,
∴∠BAD=45°;
②如图2,
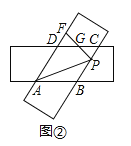
∵PF⊥AD,AD∥BC,
∴PF⊥BC,
又∵∠PCG=∠BAD=45°,
∵PC=1
∴PG=1,
∵PF=4
∴FG=PF-PG=4-1=3,
又∵∠CDF=45°=∠DGF,
∴DF=FG=3.

练习册系列答案
相关题目