��Ŀ����
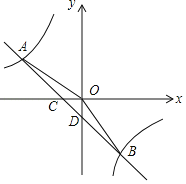
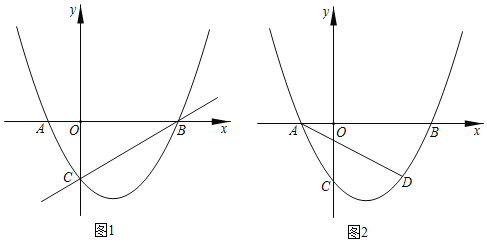
����Ŀ����ͼ1����֪������y��![]() ��x+1����x��3����mΪ��������m��0��������c��0����
��x+1����x��3����mΪ��������m��0��������c��0����![]() ������x�ύ�ڵ�A��B����Aλ�ڵ�B����ࣩ��
������x�ύ�ڵ�A��B����Aλ�ڵ�B����ࣩ��
��1����ֱ��д��m��ֵ����A����B�����ꣻ
��2������̽������ֱ��BC���Ƿ���ڵ�P��ʹ��P��A��BΪ��������������BOC���ƣ������ڣ������AP�ij����������ڣ�˵�����ɣ�
��3����ͼ2����D��2����![]() ��������AD�����������Ƿ���ڵ�Q��ʹ��BAQ��2��BAD�������ڣ���ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
��������AD�����������Ƿ���ڵ�Q��ʹ��BAQ��2��BAD�������ڣ���ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��m��![]() ��A����1��0����B��3��0������2�����ڣ�AP�ij�Ϊ2��
��A����1��0����B��3��0������2�����ڣ�AP�ij�Ϊ2��![]() ����3�����ڣ���Q������Ϊ��0����
����3�����ڣ���Q������Ϊ��0����![]() ����6��7
����6��7![]() ����
����
��������
��1������C������������ʽy��![]() ��x+1����x��3���������m��ֵ����y��0���������A��B�ĺ����ꣻ
��x+1����x��3���������m��ֵ����y��0���������A��B�ĺ����ꣻ
��2����������ۣ����Ե�PΪֱ�Ƕ���ʱ��֤��ABCΪֱ�������Σ�������BOC���ƣ����Ե�P���C�غϣ����Ե�AΪֱ�Ƕ���ʱ������A��x��Ĵ��ߣ���BC�ڵ�P�������Ƶ��������AP�ij��ȼ��ɣ����Ե�BΪֱ�Ƕ���ʱ�������ڣ�
��3����������ۣ��������BAD��30��������Q��x���·�ʱ�������BAC��60�������Q���C�غϣ�����Q��x���Ϸ�ʱ������C����x��ĶԳƵ�E��ֱ��AE����������x���Ϸ��Ľ��㼴Ϊ��Q��
��1������C��0����![]() ������y��
������y��![]() ��x+1����x��3����
��x+1����x��3����
�ã�m��![]() ��
��
�������߽���ʽΪ��y��![]() ��x+1����x��3����
��x+1����x��3����![]() x2��
x2��![]() x��
x��![]() ��
��
��y��0ʱ��x1����1��x2��3��
��A����1��0����B��3��0����
��2�����ڵ�P���������£�
����������y��![]() x2��
x2��![]() x��
x��![]() ��
�У�
��x��0ʱ��y����![]() ��
��
��C��0����![]() ����OC��
����OC��![]() ��
��
��AC2��AO2+CO2��4��BC2��BO2+CO2��12��
�֡�AB2��42��16��
��AC2+BC2��AB2��
���ABC��ֱ�������Σ�
���ACB����COB��90����
�֡ߡ�OBC����CBA��
���BOC�ס�BCA��
����P���C�غϣ�
��AP��AC��![]() ��2��
��2��
�ڹ���A��AP��x�ᣬ��ֱ��BC�ڵ�P��
��AP��OC��
���BAP�ס�BOC��
��![]() ��
��
��![]() ��
��
��AP��![]() ��
��
����������AP�ij�Ϊ2��![]() ��
��
��3�����ڵ�Q���������£�
��ͼ2������D��DH��x���ڵ�H��
��H��2��0����
�ٵ���Q��x���·�ʱ��
DH��![]() ��AH��3��
��AH��3��
����Rt��AHD��
tan��BAD��![]() ��
��
���BAD��30����
��Rt��AOC��
tan��BAC��![]() ��
��![]() ��
��
���BAC��60����
���BAC��2��BAD��
���Q���C�غϣ�
��Q1��0����![]() ����
����
�ڵ���Q��x���Ϸ�ʱ��
����C����x��ĶԳƵ�E��0��![]() ����
����
���EAB����CAB��60����2��BAD��
��ֱ��AE����������x���Ϸ��Ľ��㼴Ϊ��Q��
��ֱ��AE�Ľ���ʽΪy��kx+![]() ��
��
����A����1��0�����룬��
k��![]() ��
��
��yAE��![]() x+
x+![]() ��
��
��������![]() x+
x+![]() ��
��![]() x2��
x2��![]() x��
x��![]() ��
��
��ã�x1����1��x2��6��
��Q2��6��7![]() ����
����
������������Q��������0����![]() ����6��7
����6��7![]() ����
����